
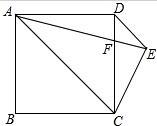
 如图,四边形ABCD为正方形,DE∥AC,AE=AC,AE与CD相交于F,试探究△CEF的形状并说明理由.
如图,四边形ABCD为正方形,DE∥AC,AE=AC,AE与CD相交于F,试探究△CEF的形状并说明理由. 分析 把△ADE顺时针旋转90°得到△ABG,从而可得B、G、D三点在同一条直线上,然后可以证明△AGB与△CGB全等,根据全等三角形对应边相等可得AG=CG,所以△AGC为等边三角形,根据等边三角形的性质可以推出∠CEF=∠CFE=75°,从而得解.
解答  解:△CEF是等腰三角形,理由如下:
解:△CEF是等腰三角形,理由如下:
如图所示,顺时针旋转△ADE90°得到△ABG,连接CG.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ADC=90°,∠ACD=45°,
∵DE∥AC,
∴∠CDE=∠ACD=45°,
∴∠ADE=90°+45°=135°,
∵∠ABG=∠ADE=135°,
∴B,G,D在一条直线上,
∴∠ABG=∠CBG=180°-45°=135°,
在△AGB与△CGB中,$\left\{\begin{array}{l}{AB=BC}&{\;}\\{∠ABG=∠CBG}&{\;}\\{BG=BG}&{\;}\end{array}\right.$,
∴△AGB≌△CGB(SAS),
∴AG=AC=GC=AE,
∴△AGC为等边三角形,
∵AC⊥BD(正方形的对角线互相垂直),
∴∠AGB=30°,
∴∠EAC=30°,
∵AE=AC,
∴∠AEC=∠ACE=$\frac{180°-30°}{2}$=75°,
又∵∠EFC=∠DFA=45°+30°=75°,
∴∠EFC=∠AEC,
∴CE=CF,
即△CEF是等腰三角形.
点评 本题综合考查了正方形的性质,全等三角形的判定,以及旋转变换的性质,根据旋转变换构造出图形是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | m2$\sqrt{m}$ | B. | -m2$\sqrt{m}$ | C. | m2$\sqrt{-m}$ | D. | -m2$\sqrt{-m}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知四边形ABCD和四边形EFGC都是正方形,且面积分别为500m2和300m2.李大爷和张大爷想在长方形AHED土地上和长方形HBGF土地上种植相同的经济作物,如果每平方米能收获3元,那么李大爷要比张大爷多收入多少元?(结果不求近似值)
如图,已知四边形ABCD和四边形EFGC都是正方形,且面积分别为500m2和300m2.李大爷和张大爷想在长方形AHED土地上和长方形HBGF土地上种植相同的经济作物,如果每平方米能收获3元,那么李大爷要比张大爷多收入多少元?(结果不求近似值)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com