
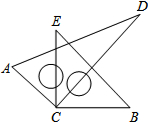
 如图所示,将一副三角尺的直角顶点C叠放在一起,
如图所示,将一副三角尺的直角顶点C叠放在一起,

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
 学校科技小组研制了一套信号发射、接收系统,在对系统进行测试中,小明从路口A处出发,沿东南方向笔直公路行进,并发射信号;小华同时从A处出发,沿西南方向笔直公路行进,并接收信号.若小华步行速度为24米/分,小明步行速度为32米/分,恰好在出发后10分钟后信号开始不清楚.求出他们研制的信号收发系统的信号传送半径?(以信号清晰为界限,请在图中画出示意图后再解答)
学校科技小组研制了一套信号发射、接收系统,在对系统进行测试中,小明从路口A处出发,沿东南方向笔直公路行进,并发射信号;小华同时从A处出发,沿西南方向笔直公路行进,并接收信号.若小华步行速度为24米/分,小明步行速度为32米/分,恰好在出发后10分钟后信号开始不清楚.求出他们研制的信号收发系统的信号传送半径?(以信号清晰为界限,请在图中画出示意图后再解答)查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,点A,B在反比例函数y=-
如图,点A,B在反比例函数y=-| 4 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com