
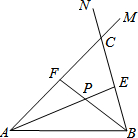
 ���߶�AB��ͬ��������AM��BN������MAB���NBA��ƽ���߷ֱ�����BN��AM�ڵ�E��F��AE��BF���ڵ�P����ͼ�����ͬѧ���ֵ�����AM��BN���ڵ�C���ҡ�ACB=60��ʱ���������������ۣ�
���߶�AB��ͬ��������AM��BN������MAB���NBA��ƽ���߷ֱ�����BN��AM�ڵ�E��F��AE��BF���ڵ�P����ͼ�����ͬѧ���ֵ�����AM��BN���ڵ�C���ҡ�ACB=60��ʱ���������������ۣ����� �����������ۣ������������εĽ�ƽ���ߺ������ε��ڽǺͼ��ɵó����ۣ�
�����жϳ���PAG�ա�PAF��SAS���ó���AFP=��AGP�����ͬ�ǵIJ�����ȼ��ɵó���BGP=��BEP�������жϳ���BPG�ա�BPE��AAS�������ɵó����ۣ�
��1���ɽ�ƽ���ߺ�ƽ�������������MAB+��NBA���Ӷ��õ���APB=90�㣬����õȱ߶ԵȽǣ����ɣ�
��2���ȸ����������AF��FG�������FAG=60�㣬��������������ۼ��㣮
��� �⣺���Ľ��ۣ��١ߡ�ACB=60�㣬
���BAC+��ABC=120�㣬
�ߡ�MAB���NBA��ƽ���߷ֱ�����BN��AM�ڵ�E��F��
���PAB+��PBA=$\frac{1}{2}$����PAB+��PBA��=60�㣬
���APB=120�㣬
����ͼ�� ��AB��ȡһ��G��ʹAG=AF��
��AB��ȡһ��G��ʹAG=AF��
��AE�ǡ�BAM�Ľ�ƽ���ߣ�
���PAG=��PAF��
�ڡ�PAG�͡�PAF�У�$\left\{\begin{array}{l}{AF=AG}\\{��PAF=��PAB}\\{AP=AP}\end{array}\right.$��
���PAG�ա�PAF��SAS����
���AFP=��AGP��
�ߡ�EPF=��APB=120�㣬��ACB=60�㣬
���EPF+��ACB=180�㣬
���PFC+��PEC=180�㣬
�ߡ�PFC+��AFP=180�㣬
���PEC=��AFP��
���PEC=��AGP��
�ߡ�AGP+��BGP=180�㣬
���PEC+��BGP=180�㣬
�ߡ�PEC+��PEB=180�㣬
���BGP=��BEP��
��BF�ǡ�ABC�Ľ�ƽ���ߣ�
���PBG=��PBE��
�ڡ�BPG�͡�BPE�У�$\left\{\begin{array}{l}{��BGP=��BEP}\\{��PBG=��PBE}\\{BP=BP}\end{array}\right.$��
���BPG�ա�BPE��AAS����
��BG=BE��
��AF+BE=AB��
��1��ԭ���ⲻ�������½���Ϊ����APB=90�㣬AF+BE=2AB����AF=BE=AB����
���ɣ���AM��BN��
���MAB+��NBA=180�㣬
��AE��BF�ֱ�ƽ�֡�MAB��NBA��
���EAB=$\frac{1}{2}$��MAB����FBA=$\frac{1}{2}$��NBA��
���EAB+��FBA=$\frac{1}{2}$����MAB+��NBA��=90�㣬
���APB=90�㣬
��AEƽ�֡�MAB��
���MAE=��BAE��
��AM��BN��
���MAE=��BAE��
���BAE=��BEA��
��AB=BE��
ͬ����AF=AB��
��AF+BE=2AB����AF=BE=AB����
��2����ͼ1��
����F��FG��AB��G��
��AF=BE��AF��BE��
���ı���ABEF��ƽ���ı��Σ�
��AF+BE=16��
��AB=AF=BE=8��
��32$\sqrt{3}$=8��FG��
��FG=4$\sqrt{3}$��
��Rt��FAG��AF=8��
���FAG=60�㣬
����G���߶�AB��ʱ����FAB=60�㣬
����G���߶�BA�ӳ���ʱ����FAB=120�㣬
����ͼ2��
����FAB=60��ʱ����PAB=30�㣬
��PB=4��PA=4$\sqrt{3}$��
��BQ=5����BPA=90�㣬
��PQ=3��
��AQ=4$\sqrt{3}$-3��AQ=4$\sqrt{3}$+3��
����ͼ3��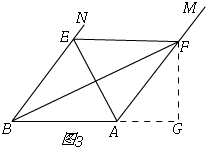
����FAB=120��ʱ����PAB=60�㣬��FBG=30�㣬
��PB=4$\sqrt{3}$��
��PB=4$\sqrt{3}$��5��
���߶�AE�ϲ����ڷ��������ĵ�Q��
�൱��FAB=60��ʱ��AQ=4$\sqrt{3}$-3��4$\sqrt{3}$+3��
���� �������ı����ۺ��⣬��Ҫ������ƽ���ߵ����ʣ���ƽ���ߵ����ʣ�ֱ�������ε����ʣ����ɶ������Ȿ��Ĺؼ����ù��ɶ��������߶Σ�


 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д� ��˼άС�ھ�100����ҵ��ϵ�д�
��˼άС�ھ�100����ҵ��ϵ�д� ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
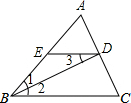 ��ͼ����ABC�У�BA=BC��BD�������εĽ�ƽ���ߣ�DE��BC��AB��E�����н��ۣ��١�1=��3����DE=$\frac{1}{2}$AB����S��ADE=$\frac{1}{4}$S��ABC����ȷ���У�������
��ͼ����ABC�У�BA=BC��BD�������εĽ�ƽ���ߣ�DE��BC��AB��E�����н��ۣ��١�1=��3����DE=$\frac{1}{2}$AB����S��ADE=$\frac{1}{4}$S��ABC����ȷ���У�������| A�� | 0�� | B�� | 1�� | C�� | 2�� | D�� | 3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | ||
| C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����֪�����ϵĵ�A��B��C��D�ֱ��ʾ��-2��1��2��3�����ʾ��5-$\sqrt{5}$�ĵ�PӦ�����߶Σ�������
��ͼ����֪�����ϵĵ�A��B��C��D�ֱ��ʾ��-2��1��2��3�����ʾ��5-$\sqrt{5}$�ĵ�PӦ�����߶Σ�������| A�� | AO�� | B�� | OB�� | C�� | BC�� | D�� | CD�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
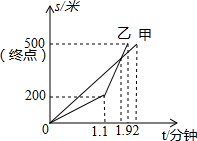 ��2015���ij��оٰ�ġ������ۣ�����硱�����У��ס��������ڱ���ʱ��·��s���ף���ʱ��t�����ӣ�֮��ĺ�����ϵͼ����ͼ��ʾ������ͼ��õ����н��ۣ����д�����ǣ�������
��2015���ij��оٰ�ġ������ۣ�����硱�����У��ס��������ڱ���ʱ��·��s���ף���ʱ��t�����ӣ�֮��ĺ�����ϵͼ����ͼ��ʾ������ͼ��õ����н��ۣ����д�����ǣ�������| A�� | ��α�����ȫ����500�� | |
| B�� | �Ҷ��ȵ����յ� | |
| C�� | ���������Ӵӳ�����1.1����ʱ��Σ��Ҷӵ��ٶȱȼӵ��ٶȿ� | |
| D�� | ���������ʱ�ҵ��ٶ���375��/���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
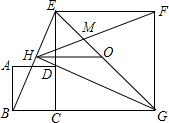 ��ͼ��������ABCD�ı���������CGFE�ı�CE�غϣ�O��EG���е㣬��EGC��ƽ����GH����D����BE�ڵ�H������OH��FH��EG��FH���ڵ�M�����������ĸ����ۣ���GH��BE��HO$\frac{��}{=}$$\frac{1}{2}$BG����GH2=GM•GE���ܡ�GBE�ס�GMF��������ȷ���У�������
��ͼ��������ABCD�ı���������CGFE�ı�CE�غϣ�O��EG���е㣬��EGC��ƽ����GH����D����BE�ڵ�H������OH��FH��EG��FH���ڵ�M�����������ĸ����ۣ���GH��BE��HO$\frac{��}{=}$$\frac{1}{2}$BG����GH2=GM•GE���ܡ�GBE�ס�GMF��������ȷ���У�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ����һ��ֱ��������ƴ����һ��õ��ı���ABCD�����С�BAC=45�㣬��ACD=30�㣬��EΪCD���ϵ��е㣬����AE������ADE��AE����ֱ�߷��۵õ���AD��E��D��E��AC��F�㣮��AB=3$\sqrt{2}$cm����
��ͼ��ʾ����һ��ֱ��������ƴ����һ��õ��ı���ABCD�����С�BAC=45�㣬��ACD=30�㣬��EΪCD���ϵ��е㣬����AE������ADE��AE����ֱ�߷��۵õ���AD��E��D��E��AC��F�㣮��AB=3$\sqrt{2}$cm�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com