
【题目】如图所示,若将类似于a、b、c、d四个图的图形称做平面图,则其顶点数、边数与区域数之间存在某种关系.观察图b和表中对应的数值,探究计数的方法并作答.

(1)数一数每个图中各有多少个顶点、多少条边,这些边围出多少个区域并填表:
平面图 | a | b | c | d |
顶点数(S) | 7 | |||
边数(M) | 9 | |||
区域数(N) | 3 |
(2)根据表中数值,写出平面图的顶点数、边数、区域数之间的一种关系为 ;
(3)如果一个平面图有20个顶点和11个区域,那么利用(2)中得出的关系可知这个平面图有 条边.
【答案】(1)填表见解析;(2)S+N-M=1;(3)30.
【解析】试题分析:(1)按照自己熟悉的规律去数顶点数,边数以及区域数;
(2)4+3-6=1,7+3-9=1,8+5-12=1,10+6-15=1,所以可得到一般规律:顶点数+区域数一边数=1;
(3)边数=顶点数+区域数-1.
试题解析:(1)数一数每个图中各有多少个顶点、多少条边,这些边围出多少个区域并填表:
平面图 | a | b | c | d |
顶点数(S) | 4 | 7 | 8 | 10 |
边数(M) | 6 | 9 | 12 | 15 |
区域数(N) | 3 | 3 | 5 | 6 |
(2)观察表中数据可得;4+36=1,7+39=1,8+512=1,10+615=1
∴S+NM=1;(或顶点数+区域数一边数=1)
故答案为:S+NM=1;
(3)由(2)得:边数=顶点数+区域数1=20+111=30.
故答案为:30.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】对![]() ,
, ![]() 定义一种新运算
定义一种新运算![]() ,规定
,规定![]() (其中
(其中![]() ,
, ![]() 均为非零常数),这里等式右边是通常的四则运算,例:
均为非零常数),这里等式右边是通常的四则运算,例: ![]() .
.
已知![]() ,
, ![]() .
.
(1)求![]() ,
, ![]() 的值;
的值;
(2)若关于m的不等式组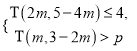 恰好有3个整数解,求实数
恰好有3个整数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx﹣4k+5的图象与反比例函数y= ![]() (x>0)的图象相交于点A(p,q).当一次函数y的值随x的值增大而增大时,p的取值范围是 .
(x>0)的图象相交于点A(p,q).当一次函数y的值随x的值增大而增大时,p的取值范围是 . 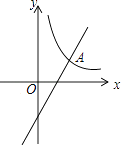
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红同学在做作业时,遇到这样一道几何题:
已知:AB∥CD∥EF,∠A=110°,∠ACE=100°,过点E作EH⊥EF,垂足为E,交CD于H点.
(1)依据题意,补全图形;
(2)求∠CEH的度数.
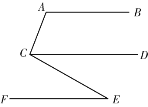
小明想了许久对于求∠CEH的度数没有思路,就去请教好朋友小丽,小丽给了他如图2所示的提示:

请问小丽的提示中理由①是 ;
提示中②是: 度;
提示中③是: 度;
提示中④是: ,理由⑤是 .
提示中⑥是 度;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中错误的是( )
A. 若∠C=∠A–∠B,则△ABC为直角三角形
B. 若a∶b∶c=2∶2∶2![]() ,则△ABC为直角三角形
,则△ABC为直角三角形
C. 若a=![]() c,b=
c,b=![]() c,则△ABC为直角三角形
c,则△ABC为直角三角形
D. 若∠A∶∠B∶∠C=3∶4∶5,则△ABC为直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场对一种新售的手机进行市场问卷调查,其中一个项目是让每个人按A(不喜欢)、B(一般)、C(不比较喜欢)、D(非常喜欢)四个等级对该手机进行评价,图①和图②是该商场采集数据后,绘制的两幅不完整的统计图,请你根据以上统计图提供的信息,回答下列问题:
(1)本次调查的人数为多少人?A等级的人数是多少?请在图中补全条形统计图.
(2)图①中,a等于多少?D等级所占的圆心角为多少度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3, ![]() ),点C的坐标为(
),点C的坐标为(![]() ,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )
,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6,AD=10,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,AG=2.5,则△CEF的周长为

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com