

分析 (1)要证明AG平分∠FAB,只要证明△AFG≌△ABG即可,根据题目中的信息,可以得到两个三角形全等的条件,从而可以证明结论成立;
(2)可以通过旋转将DE和BH放在同一条直线上,根据题目中的信息可以得到线段DE、AH、BH三者之间的数量关系..
解答 (1)证明:∵四边形ABCD是正方形,
∴AD=AB,∠B=∠ADC=∠ADE=90°,
∵△AEF是由△AED翻折得到,
∴AF=AD,∠F=∠ADE=90°,
∴AF=AB,∠F=∠B=90°,
在Rt△AFG和Rt△ABG中,
$\left\{\begin{array}{l}{AF=AB}\\{AG=AG}\end{array}\right.$,
∴Rt△AFG≌Rt△ABG(HL),
∴∠FAG=∠BAG,
∴AG平分∠FAB;
(2)如图2中,将△ADE绕点A顺时针旋转90°得到△ABM,
∴∠ADE=∠ABM=90°,∠EAM=90°,DE=BM,
∴∠FAE+∠HAM=90°,
∵△AEF是由△AED翻折得到,
∴∠FAE=∠EAD,DE=EF,
∴∠DAM=∠HAM,
∵AD∥BC,
∴∠DAM=∠AMH,
∴∠HAM=∠AMH,
∴HA=HM,
∵HM=BH+BM,BM=DE,
∴AH=BH+DE.
点评 本题考查翻折变化、正方形的性质,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源:2016-2017学年江苏省无锡市八年级3月份阶段性检测数学试卷(解析版) 题型:填空题
如图,矩形ABCD中,AB=4,BC=5,AF平分∠DAE,EF⊥AE,则CF= .

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
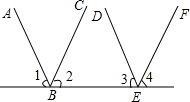 完成下列推理说明:
完成下列推理说明:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 △ABC是⊙O的内接三角形,BC=$\sqrt{3}$.如图,若AC是⊙O的直径,∠BAC=60°,延长BA到点D,使得DA=$\frac{1}{2}$BA,过点D作直线l⊥BD,垂足为点D,请将图形补充完整,判断直线l和⊙O的位置关系并说明理由.
△ABC是⊙O的内接三角形,BC=$\sqrt{3}$.如图,若AC是⊙O的直径,∠BAC=60°,延长BA到点D,使得DA=$\frac{1}{2}$BA,过点D作直线l⊥BD,垂足为点D,请将图形补充完整,判断直线l和⊙O的位置关系并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:点C在线段AE上,线段AC=6,线段CE=4,点B、D分别是AC、CE的中点,求线段BD的长度.
已知:点C在线段AE上,线段AC=6,线段CE=4,点B、D分别是AC、CE的中点,求线段BD的长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com