
【题目】已知二次函数y=-x2-2x+3.
(1)将其配方成y=a(x-k)2+h的形式,并写出它的开口方向、对称轴及顶点坐标.
(2)在平面直角坐标系中画出函数的图象,并观察图象,当y≥0时,x的取值范围.
【答案】(1)y=-(x+1)2+4;开口向下,对称轴是直线x=-1,顶点坐标为(-1,4);(2)图像见解析;y≥0时,-3≤x≤1.
【解析】
(1)根据题目中的函数解析式,利用配方法可以将题目中的函数解析式化为y=a(x-k)2+h的形式,并写出它的开口方向、对称轴及顶点坐标;
(2)根据题目中的函数解析式可以画出函数的图象,并直接写出当y≥0时,x的取值范围.
(1)二次函数y=-x2-2x+3=-(x+1)2+4,
故该函数的开口向下,对称轴是直线x=-1,顶点坐标为(-1,4);
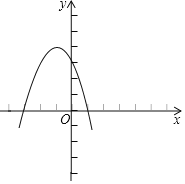
(2)当y=0时,0=-x2-2x+3,得x=-3或x=1,
故该函数的图象如右图所示,
当y≥0时,x的取值范围是-3≤x≤1.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=8,BC=6,分别以AB、BC、CA为一边向形外作正方形,连接EF、GM、ND, 设△AEF,△CGM,△BND的面积分别为![]() ,
,![]() ,
,![]() ,则
,则![]() =___.
=___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,CA=CB,CD=CE,∠ACB=∠DCE=α.
(1)求证:BE=AD;

(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
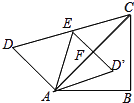
【题目】如图,将一副直角三角板拼在一起得四边形ABCD,∠ACB=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F点,若AB= 6![]() cm,点D′到BC的距离是( )
cm,点D′到BC的距离是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
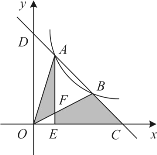
【题目】如图,一次函数 y=-x+b 与反比例函数y=![]() (x>0)的图象交于 A,B 两点,与 x 轴、y轴分别交于C,D 两点,连接 OA,OB,过 A 作 AE⊥x 轴于点 E,交 OB 于点F,设点 A 的横坐标为 m. 若 S△OAF+S 四边形 EFBC=4,则 m 的值是( )
(x>0)的图象交于 A,B 两点,与 x 轴、y轴分别交于C,D 两点,连接 OA,OB,过 A 作 AE⊥x 轴于点 E,交 OB 于点F,设点 A 的横坐标为 m. 若 S△OAF+S 四边形 EFBC=4,则 m 的值是( )
A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com