
如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.
(1)求C点坐标;
(2)求直线MN的解析式;
(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.
(1)C(0,6);(2)y=- x+6;(3)P1(4,3),P2(-
x+6;(3)P1(4,3),P2(- ,
,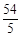 ),P3(
),P3( ,
,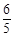 ),P4(
),P4(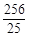 ,-
,-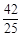 ).
).
解析试题分析:
(1)通过解方程x2﹣14x+48=0可以求得OC=6,OA=8.则C(0,6);
(2)设直线MN的解析式是y=kx+b(k≠0).把点A、C的坐标分别代入解析式,列出关于系数k、b的方程组,通过解方程组即可求得它们的值;
(3)需要分类讨论:PB为腰,PB为底两种情况下的点P的坐标.根据等腰三角形的性质、两点间的距离公式以及一次函数图象上点的坐标特征进行解答.
试题解析:
(1)解方程x2-14x+48=0得
x1=6,x2=8
∵OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根
∴OC=6,OA=8
∴C(0,6)
(2)设直线MN的解析式是y=kx+b(k≠0)
由(1)知,OA=8,则A(8,0)
∵点A、C都在直线MN上
∴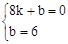
解得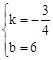 ,
,
∴直线MN的解析式为y=- x+6
x+6
(3)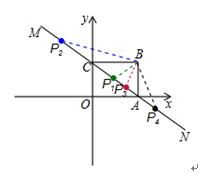
∵A(8,0),C(0,6)
∴根据题意知B(8,6)
∵点P在直线MN y=- x+6上
x+6上
∴设P(a,-- a+6)
a+6)
当以点P,B,C三点为顶点的三角形是等腰三角形时,需要分类讨论:
①当PC=PB时,点P是线段BC的中垂线与直线MN的交点,则P1(4,3);
②当PC=BC时,a2+(- a+6-6)2=64
a+6-6)2=64
解得,a=± ,则P2(-
,则P2(- ,
,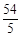 ),P3(
),P3( ,
,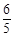 )
)
③当PB=BC时,(a-8)2+(- a+6-6)2=64
a+6-6)2=64
解得,a=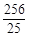 ,则-
,则- a+6=-
a+6=-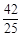
∴P4(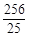 ,
,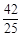 )
)
综上所述,符合条件的点P有:P1(4,3),P2(- ,
,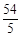 ),P3(
),P3( ,
,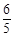 ),P4(
),P4(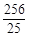 ,-
,-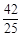 )
)
考点:一次函数综合题.


科目:初中数学 来源: 题型:解答题
如图,一次函数y1=x+1的图象与反比例函数 (k为常数,且
(k为常数,且 )的图象都经过点A(m,2).
)的图象都经过点A(m,2).
(1)求点A的坐标及反比例函数的解析式;
(2)观察图象,当x>0时,直接写出y1与y2的大小关系.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某食品加工厂需要一批食品包装盒,供应这种包装盒有两种方案可供选择:
方案1:从包装盒加工厂直接购买,购买所需的费用y1与包装盒数x满足如图的函数关系。
方案2:租凭机器自己加工,所需费用y2(包括租凭机器的费用和生产包装盒的费用)
与包装盒数 满足如图的函数关系。
满足如图的函数关系。
根据图象回答下列问题:
(1)方案1中每个包装盒的价格是多少元?
(2)方案2中租凭机器的费用是多少元?生产一个包装盒的费用是多少元?
(3)请分别求出y1,y2,与x的函数表达式
(4)如果你是决策者,你认为应该选择哪种方案更省钱?并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某校实行学案式教学,需印制若干份数学学案。印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要。两种印刷方式的费用y(元)与印刷份数x(份)之间的函数关系如图所示:
(1)填空:甲种收费方式的函数关系式是 .
乙种收费方式的函数关系式是 .
(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
甲、乙两地之间有一条笔直的公路L,小明从甲地出发沿公路ι步行前往乙地,同时小亮从乙地出发沿公路L骑自行车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上小明后两人一起步行到乙地.设小明与甲地的距离为y1米,小亮与甲地的距离为y2米,小明与小亮之间的距离为s米,小明行走的时间为x分钟.y1、y2与x之间的函数图象如图1,s与x之间的函数图象(部分)如图2.
(1)求小亮从乙地到甲地过程中y1(米)与x(分钟)之间的函数关系式;
(2)求小亮从甲地返回到与小明相遇的过程中s(米)与x(分钟)之间的函数关系式;
(3)在图2中,补全整个过程中s(米)与x(分钟)之间的函数图象,并确定a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某生物小组观察一植物生长,得到植物高度y(单位:厘米)与观察时间x(单位:天)的关系,并画出如图所示的图象(AC是线段,直线CD平行x轴).
(1)该植物从观察时起,多少天以后停止长高?
(2)求直线AC的解析式,并求该植物最高长多少厘米?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
华联超市欲购进A、B两种品牌的书包共400个。已知两种书包的进价和售价如下表所示。设购进A种书包x个,且所购进的两种书包能全部卖出,获得的总利润为w元。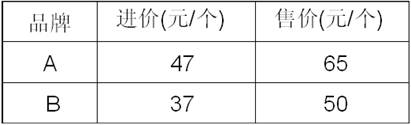
(1)求w关于x的函数关系式;
(2)如果购进两种书包的总费不超过18000元,那么该商场如何进货才能获得最大利润?并求出最大利润。
(提示利润= 售价-进价)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
为提醒人们节约用水,及时修好漏水的水龙头.两名同学分别做了水龙头漏水实验,他们用于接水的量筒最大容量为100毫升.
实验一:小王同学在做水龙头漏水实验时,每隔10秒观察量筒中水的体积,记录的数据如表(漏出的水量精确到1毫升):
| 时间t(秒) | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| 漏出的水量V(毫升) | 2 | 5 | 8 | 11 | 14 | 17 | 20 |


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com