
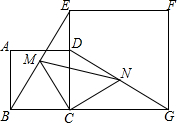
 如图,四边形ABCD和四边形ECGF都是正方形,M,N分别是线段BE和GD的中点,判断△CMN的形状,并说明理由.
如图,四边形ABCD和四边形ECGF都是正方形,M,N分别是线段BE和GD的中点,判断△CMN的形状,并说明理由. 分析 由四边形ABCD和四边形CEFG都是正方形,根据正方形的性质可得:CB=CD,CE=CG,∠BCD=∠ECG=90°,利用SAS即可证得△CBE≌△CDG,根据全等三角形的对应边相等,即可证得BE=DG,进而证明即可.
解答 解:△CMN是等腰三角形,理由如下:
∵四边形ABCD和四边形CEFG都是正方形,
∴CB=CD,CE=CG,∠BCD=∠ECG=90°,
在△CBE和△CDG中,
$\left\{\begin{array}{l}{CB=CD}\\{∠BCD=∠ECG=90°}\\{CE=CG}\end{array}\right.$,
∴△CBE≌△CDG(SAS),
∴BE=DG,
∵M,N分别是线段BE和GD的中点,
∴BM=ME=CM=$\frac{1}{2}$BE,CD=CN=NG=$\frac{1}{2}$DG,
∴CM=CN,
∴△CMN是等腰三角形.
点评 此题考查了正方形的性质与全等三角形的判定与性质.此题难度不大,注意数形结合思想的应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
 如图是长度为10米,直径为2米的水管的截面,若水管积水深度为0.5米,则水管中共积水$\frac{10π}{3}$-$\frac{5\sqrt{3}}{2}$ 立方米.
如图是长度为10米,直径为2米的水管的截面,若水管积水深度为0.5米,则水管中共积水$\frac{10π}{3}$-$\frac{5\sqrt{3}}{2}$ 立方米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
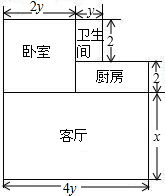 小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com