
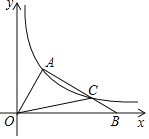
【题目】如图,在平面直角坐标系xOy中,△OAB的边OB在x轴上,过点A的反比例函数y=![]() 的图象交AB于点C,且AC:CB=2:1,S△OAC=
的图象交AB于点C,且AC:CB=2:1,S△OAC=![]() ,则k的值为( )
,则k的值为( )
A.![]() B.
B.![]() C.2D.2
C.2D.2![]()
【答案】B
【解析】
设C(a,b),根据题意则A(![]() a,3b),然后根据S△OAC=S梯形AMNC+S△OAMS△CON=S梯形AMNC,得到
a,3b),然后根据S△OAC=S梯形AMNC+S△OAMS△CON=S梯形AMNC,得到![]() (3b+b)(a
(3b+b)(a![]() a)=
a)=![]() ,即可求得k=ab=
,即可求得k=ab=![]() .
.
设C(a,b),
作AM⊥x轴于M,CN⊥x轴于N,
∴ON=a,CN=b,
∵CN∥AM,
∴△BCN∽△BAM,
∴![]() ,
,
∵AC:CB=2:1,
∴BC:AB=1:3,
∴AM=3CN=3b,
∵点A的反比例函数y=![]() 的图象交AB于点C,
的图象交AB于点C,
∴OMAM=OCN=k,
∴OM=![]() ON=
ON=![]() a,
a,
∵S△OAC=S梯形AMNC+S△OAM﹣S△CON=S梯形AMNC,
∴S梯形AMNC=![]() (3b+b)(a
(3b+b)(a![]() a)=
a)=![]() ,
,
∴k=ab=![]() ,
,
故选:B.


科目:初中数学 来源: 题型:
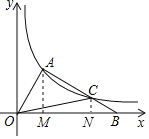
【题目】如图,BD是平行四边形ABCD的对角线,DE⊥AB于点E,过点E的直线交BC于点G,且BG=CG.
(1)求证:GD=EG.
(2)若BD⊥EG垂足为O,BO=2,DO=4,画出图形并求出四边形ABCD的面积.
(3)在(2)的条件下,以O为旋转中心顺时针旋转△GDO,得到△G′D'O,点G′落在BC上时,请直接写出G′E的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
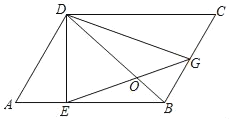
【题目】如图1,在Rt△ABC中,∠C=90°,AC=BC=2,点D、E分别在边AC、AB上,AD=DE=![]() AB,连接DE.将△ADE绕点A逆时针方向旋转,记旋转角为θ.
AB,连接DE.将△ADE绕点A逆时针方向旋转,记旋转角为θ.
(1)问题发现
①当θ=0°时,![]() = ;
= ;
②当θ=180°时,![]() = .
= .
(2)拓展探究
试判断:当0°≤θ<360°时,![]() 的大小有无变化?请仅就图2的情形给出证明;
的大小有无变化?请仅就图2的情形给出证明;
(3)问题解决
①在旋转过程中,BE的最大值为 ;
②当△ADE旋转至B、D、E三点共线时,线段CD的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
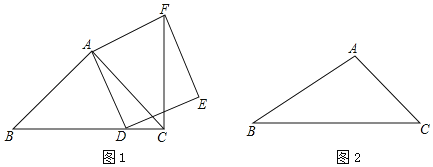
【题目】在△ABC中,∠ACB=45°,点D为射线BC上一动点(与点B、C不重合),连接AD,以AD为一边在AD右侧作正方形ADEF.
(1)如果AB=AC,如图1,且点D在线段BC上运动,判断∠BAD ∠CAF(填“=”或“≠”),并证明:CF⊥BD
(2)如果AB≠AC,且点D在线段BC的延长线上运动,请在图2中画出相应的示意图,此时(1)中的结论是否成立?请说明理由;
(3)设正方形ADEF的边DE所在直线与直线CF相交于点P,若AC=4![]() ,CD=2,求线段CP的长.
,CD=2,求线段CP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
A型利润(元/件) | B型利润(元/件) | |
甲店 | 180 | 150 |
乙店 | 120 | 110 |
(1)设分配给甲店A型产品x件,这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并写出x的取值范围;
(2)若要求总利润超过14960元,有多少种不同分配方案?请列出具体方案;
(3)为了促销,公司决定仅对甲店A型产品让利销售,每件让利a元,但让利后A型产品的每件利润仍高于甲店B型产品的每件利润,甲店的B型产品以及乙店的A,B型产品的每件利润不变,该公司如何设计分配方案,使总利润达到最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ABC=90°,BD为∠ABC的角平分线,F为AC的中点,AE∥BC交BD的延长线于点E,其中∠FBC=2∠FBD.
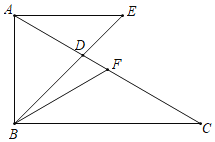
(1)求∠EDC的度数.
(2)求证:BF=AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,AB=4,D、E分别为射线CB、AC上的两动点,且BD=CE,直线AD和BE相交于M点,则CM的最大值为( )
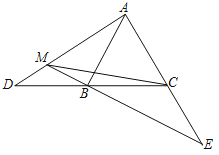
A.2![]() B.
B.![]() C.3
C.3![]() D.4
D.4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】坚持农业农村优先发展,按照产业兴旺、生态宜居的总要求,统筹推进农村经济建设.洛宁县某村出售特色水果(苹果).规定如下:
品种 | 购买数量低于50箱 | 购买数量不低于50箱 |
新红星 | 原价销售 | 以八折销售 |
红富士 | 原价销售 | 以九折销售 |
如果购买新红星40箱,红富士60箱,需付款4300元;如果购买新红星100箱,红富士35箱,需付款4950元.
(1)每箱新红星、红富士的单价各多少元?
(2)某单位需要购置这两种苹果120箱,其中红富士的数量不少于新红星的一半,并且不超过60箱,如何购买付款最少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
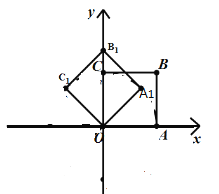
【题目】如图,在平面直角坐标系中,将正方形![]() 绕点
绕点![]() 逆时针旋转45°后得到正方形
逆时针旋转45°后得到正方形![]() .依此方式,绕点
.依此方式,绕点![]() 连续旋转2020次,得到正方形
连续旋转2020次,得到正方形![]() ,如果点
,如果点![]() 的坐标为
的坐标为![]() ,那么点
,那么点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com