
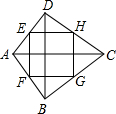
 如图,四边形ABCD中,对角线AC⊥BD,且AC=BD,点E、F、G、H分别是AD、AB、BC、CD的中点.求证:四边形EFGH是正方形.
如图,四边形ABCD中,对角线AC⊥BD,且AC=BD,点E、F、G、H分别是AD、AB、BC、CD的中点.求证:四边形EFGH是正方形. 分析 先由三角形的中位线定理求出四边相等,然后由AC⊥BD入手,进行正方形的判断.
解答 证明:在△ABC中,F、G分别是AB、BC的中点,
故可得:FG=$\frac{1}{2}$AC,同理EH=$\frac{1}{2}$AC,GH=$\frac{1}{2}$BD,EF=$\frac{1}{2}$BD,
在四边形ABCD中,AC=BD,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
在△ABD中,E、H分别是AD、CD的中点,
则EH∥AC,
同理GH∥BD,
又∵AC⊥BD,
∴EH⊥HG,
∴四边形EFGH是正方形.
点评 此题考查了正方形的判定,解题的关键是了解既是矩形又是菱形的四边形是正方形,难度适中.


科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
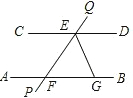 如图,AB∥CD,直线PQ分别交AB、CD于点E、F,EG是∠FED的平分线,交AB于点G.若∠QED=40°,那么∠EGB等于110°.
如图,AB∥CD,直线PQ分别交AB、CD于点E、F,EG是∠FED的平分线,交AB于点G.若∠QED=40°,那么∠EGB等于110°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{25}$=±5 | B. | ±$\sqrt{25}$=5 | C. | $\sqrt{{({-5})}^2}$=5 | D. | $\sqrt{{({-3})}^2}$=-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,阳光下斜坡旁有一棵树AB,它的阴影投在斜坡上为AC=10米,斜坡与平面形成的坡角∠DAC=15°,光线与斜坡形成的∠BCA=75°.求树AB的高度(精确到0.1米)参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,$\sqrt{3}$≈1.73.
如图,阳光下斜坡旁有一棵树AB,它的阴影投在斜坡上为AC=10米,斜坡与平面形成的坡角∠DAC=15°,光线与斜坡形成的∠BCA=75°.求树AB的高度(精确到0.1米)参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,$\sqrt{3}$≈1.73.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
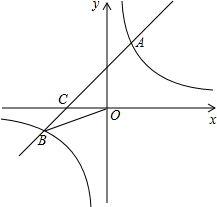 如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC=$\frac{1}{2}$.
如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC=$\frac{1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com