
【题目】如图,在平面直角坐标系中,点![]() 的坐标
的坐标 ,将线段
,将线段![]() 绕点
绕点![]() 按顺时针方向旋转45°,再将其长度伸长为
按顺时针方向旋转45°,再将其长度伸长为![]() 的2倍,得到线段
的2倍,得到线段![]() ;又将线段
;又将线段![]() 绕点
绕点![]() 按顺时针方向旋转45°,长度伸长为
按顺时针方向旋转45°,长度伸长为![]() 的2倍,得到线段
的2倍,得到线段![]() ;如此下去,得到线段
;如此下去,得到线段![]() 、
、![]() ,……,
,……,![]() (
(![]() 为正整数),则点
为正整数),则点![]() 的坐标是_________.
的坐标是_________.
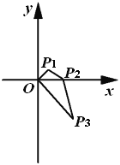
【答案】(0,-22019)
【解析】
根据题意得出OP1=1,OP2=2,OP3=4,如此下去,得到线段OP3=4=22,OP4=8=23…,OPn=2n-1,再利用旋转角度得出点P2020的坐标与点P4的坐标在同一直线上,进而得出答案.
解:∵点P1的坐标为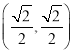 ,将线段OP1绕点O按顺时针方向旋转45°,再将其长度伸长为OP1的2倍,得到线段OP1;
,将线段OP1绕点O按顺时针方向旋转45°,再将其长度伸长为OP1的2倍,得到线段OP1;
∴OP1=1,OP2=2,
∴OP3=4,如此下去,得到线段OP4=23,OP5=24…,
∴OPn=2n-1,
由题意可得出线段每旋转8次旋转一周,
∵2020÷8=252…4,
∴点P2020的坐标与点P4的坐标在同一直线上,正好在y轴负半轴上,
∴点P2020的坐标是(0,-22019).
故答案为:(0,-22019).


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
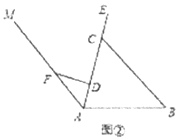
【题目】随州市新水一桥(如图1)设计灵感来源于市花﹣﹣兰花,采用蝴蝶兰斜拉桥方案,设计长度为258米,宽32米,为双向六车道,2018年4月3日通车.斜拉桥又称斜张桥,主要由索塔、主梁、斜拉索组成.某座斜拉桥的部分截面图如图2所示,索塔AB和斜拉索(图中只画出最短的斜拉索DE和最长的斜拉索AC)均在同一水平面内,BC在水平桥面上.已知∠ABC=∠DEB=45°,∠ACB=30°,BE=6米,AB=5BD.
(1)求最短的斜拉索DE的长;
(2)求最长的斜拉索AC的长.
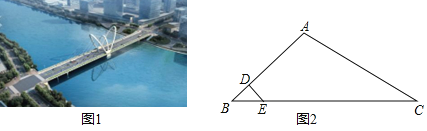
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春天来了,石头城边,秦淮河畔,鸟语花香,柳条飘逸.为给市民提供更好的休闲锻炼环境,决定对一段总长为1800米的外秦淮河沿河步行道出新改造,该任务由甲、乙两工程队先后接力完成.甲工程队每天改造12米,乙工程队每天改造8米,共用时200天.
(1)根据题意,小莉、小刚两名同学分别列出尚不完整的方程组如下:
小莉:![]() 小刚:
小刚:
根据两名同学所列的方程组,请你分别指出未知数x、y表示的意义,然后在方框中补全小莉、小刚两名同学所列的方程组:
小莉:x表示 ,y表示 ;
小刚:x表示 ,y表示 .
(2)求甲、乙两工程队分别出新改造步行道多少米.
查看答案和解析>>
科目:初中数学 来源: 题型:
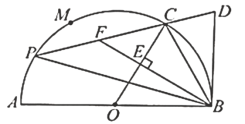
【题目】如图,![]() 为半⊙O的直径,
为半⊙O的直径,![]() ,
,![]() 是半圆上的三等分点,
是半圆上的三等分点,![]() ,
,![]() 与半⊙O相切于点
与半⊙O相切于点![]() ,点
,点![]() 为
为![]() 上一动点(不与点
上一动点(不与点![]() ,
,![]() 重合),直线
重合),直线![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,则下列结论正确的是______________.(写出所有正确结论的序号)
,则下列结论正确的是______________.(写出所有正确结论的序号)
①![]() ;②
;②![]() 的长为
的长为![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 为定值.
为定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如表是一个4×4(4行4列共16个“数”组成)的奇妙方阵,从这个方阵中选四个“数”,而且这四个“数”中的任何两个不在同一行,也不在同一列,有很多选法,把每次选出的四个“数”相加,其和是定值,则方阵中第三行三列的“数”是( )
30 |
| 2 | 22 |
﹣3 | ﹣2 | ﹣ | 0 |
|﹣5| | 6 | 23 | |
( | 4 |
| ( |
A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=15,AC=20,tanA=![]() ,点P在AB边上,⊙P的半径为定长.当点P与点B重合时,⊙P恰好与AC边相切;当点P与点B不重合时,⊙P与AC边相交于点M和点N.
,点P在AB边上,⊙P的半径为定长.当点P与点B重合时,⊙P恰好与AC边相切;当点P与点B不重合时,⊙P与AC边相交于点M和点N.
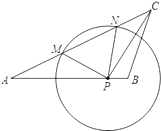
(1)求⊙P的半径;
(2)当AP=![]() 时,试探究△APM与△PCN是否相似,并说明理由.
时,试探究△APM与△PCN是否相似,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是以原点
是以原点![]() 为对称中心的矩形,
为对称中心的矩形,![]() ,
,![]() ,
,![]() 和
和![]() 分别与
分别与![]() 轴交于点
轴交于点![]() 、
、![]() ,连接
,连接![]() .
.

(1)写出点![]() 和点
和点![]() 的坐标;
的坐标;
(2)求四边形![]() 的面积;
的面积;
(3)判断点![]() 在矩形
在矩形![]() 的内部还是外部;
的内部还是外部;
(4)要使直线![]() 与矩形
与矩形![]() 没有公共点,直接写出
没有公共点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“4000辆自行车、187个服务网点”,某市区现已实现公共自行车服务全覆盖,为人们的生活带来了方便。图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A,D,C,E在同一条直线上,CD=30 cm,DF=20 cm,AF=25 cm,FD⊥AE于点D,座杆CE=15 cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com