
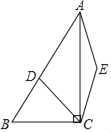
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=4,D是AB上一个动点,将点D绕点C顺时针旋转60°,得到点E,连接AE.若AE=![]() ,则BD=_____.
,则BD=_____.
【答案】1或3
【解析】
取AB中点F,连接EF交直线EF交AC于点K.分点E在△ABC内部或外部两种情形分别求解即可.
解:取AB中点F,连接EF交直线EF交AC于点K.
情形1:当点E在△ABC内部时,如图1中,连接CF,DE.
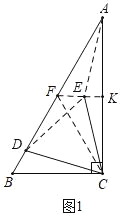
在Rt△ABC中,∵∠ACB=90°,∠BAC=30°,BC=4,
∴AB=2BC=8,AC=![]() BC=4
BC=4![]() ,
,
∵AF=FB,
∴CF=BF=AF,
∵∠B=60°,
∴△BCF是等边三角形,
∴CF=CB,∠BCF=60°,
∵CD=CE,∠DCE=60°,
∴∠BCF=∠DCE,
∴∠BCD=∠FCE,
∴△BCD≌△FCE(SAS),
∴BD=EF,∠B=∠CFE=60°,
∴∠CFE=∠BCF=60°,
∴EF∥BC,
∵AF=FB,
∴AK=CK=2![]() ,FK=
,FK=![]() BC=2,
BC=2,
在Rt△AEK中,EK=![]() =1,
=1,
∴EF=FK﹣EK=1.
情形2:当点E在△ABC外部时,同法可得:BD=EF=FK+EK=2+1=3,
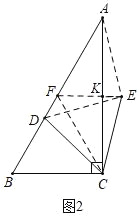
故答案为1或3.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
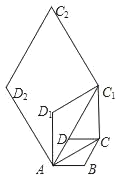
【题目】 如图,作出边长为1的菱形ABCD,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,连接AC1,再以AC1为边作第三个菱形ACC2D2,使∠D2AC1=60°;…按此规律所作的第2019个菱形的边长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
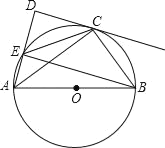
【题目】如图,AB是⊙O的直径,CD切⊙O于点C,AD交⊙O于点E,AC平分∠BAD,连接BE.
(1)求证:CD⊥ED;
(2)若CD=4,AE=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
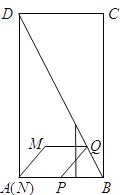
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 两点分别从
两点分别从![]() ,
,![]() 同时出发,点
同时出发,点![]() 沿折线
沿折线![]() 运动,在
运动,在![]() 上的速度是2
上的速度是2![]() /
/![]() ,在BC上的速度是
,在BC上的速度是![]()
![]() /
/![]() ;点
;点![]() 在
在![]() 上以2
上以2![]() /
/![]() 的速度向终点
的速度向终点![]() 运动,过点
运动,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .连结
.连结![]() ,以
,以![]() ,
,![]() 为邻边作平行四边形
为邻边作平行四边形![]() .设运动的时间为
.设运动的时间为![]() (s),平行四边形
(s),平行四边形![]() 与矩形
与矩形![]() 重叠部分的图形面积为
重叠部分的图形面积为![]()
![]()
(1)当![]() ⊥
⊥![]() 时,求
时,求![]() 的值;
的值;
(2)求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)直线![]() 将矩形
将矩形![]() 的面积分成1∶3两部分时,求
的面积分成1∶3两部分时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级某班同学为了了解2012年某居委会家庭月均用水情况,随机调查了该居委会部分家庭,并将调查数据进行如下调整:
月均用水量x(t) | 频数(户) | 频率 |
0<x≤5 | 6 | 0.12 |
5<x≤10 | a | 0.24 |
10<x≤15 | 16 | 0.32 |
15<x≤20 | 10 | 0.20 |
20<x≤25 | 4 | 0.08 |
25<x≤30 | 2 | 0.04 |
请解答以下问题:
(1)频数分布表中a= ,把频数分布直方图补充完整;
(2)求该居委会用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该居委会有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?

查看答案和解析>>
科目:初中数学 来源: 题型:
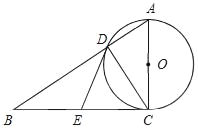
【题目】如图,在Rt△ABC中,∠ACB=90°,E是BC的中点,以AC为直径的⊙O与AB边交于点D,连接DE.
(1)求证:DE是⊙O的切线;
(2)若CD=6cm,DE=5cm,求⊙O直径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
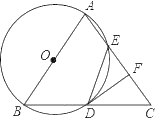
【题目】如图,在△ABC中,AB=AC,AB是⊙O的直径,⊙O与BC交于点D,⊙O与AC交于点E,DF⊥AC于F,连接DE.
(1)求证:D为BC中点;
(2)求证:DF与⊙O相切;
(3)若⊙O的半径为5,tan∠C=![]() ,则DE= .
,则DE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
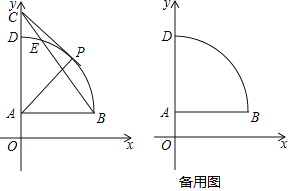
【题目】如图,A(0,2),B(6,2),C(0,c)(c>0),以A为圆心AB长为半径的![]() 交y轴正半轴于点D,
交y轴正半轴于点D,![]() 与BC有交点时,交点为E,P为
与BC有交点时,交点为E,P为![]() 上一点.
上一点.
(1)若c=6![]() +2,
+2,
①BC= ,![]() 的长为 ;
的长为 ;
②当CP=6![]() 时,判断CP与⊙A的位置关系,井加以证明;
时,判断CP与⊙A的位置关系,井加以证明;
(2)若c=10,求点P与BC距离的最大值;
(3)分别直接写出当c=1,c=6,c=9,c=11时,点P与BC的最大距离(结果无需化简)
查看答案和解析>>
科目:初中数学 来源: 题型:
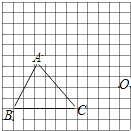
【题目】在如图的方格纸中(每个小方格的边长都是1个单位)有一点O和△ABC.
(1)请以点O为位似中心,把△ABC缩小为原来的一半(不改变方向),得到△A′B′C′;
(2)请用适当的方式描述△A′B′C′的顶点A′、B′、C′的位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com