
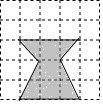
 如图,方格图中小正方形的边长为1.将方格图中阴影部分图形剪下来,再把剪下的阴影部分重新剪拼成一个正方形(不重叠无缝隙),那么所拼成的这个正方形的边长为$\sqrt{6}$.
如图,方格图中小正方形的边长为1.将方格图中阴影部分图形剪下来,再把剪下的阴影部分重新剪拼成一个正方形(不重叠无缝隙),那么所拼成的这个正方形的边长为$\sqrt{6}$.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
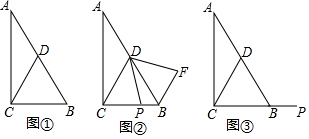
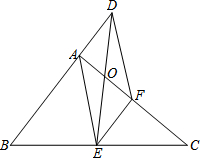 在Rt△ABC中,∠BAC=90°,E、F分别是BC、AC的中点,延长BA到点D,使AB=2AD,连接DE、DF、AE、EF,AF与DE交于点O.
在Rt△ABC中,∠BAC=90°,E、F分别是BC、AC的中点,延长BA到点D,使AB=2AD,连接DE、DF、AE、EF,AF与DE交于点O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
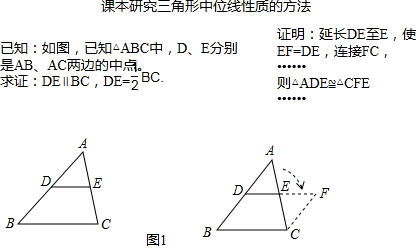
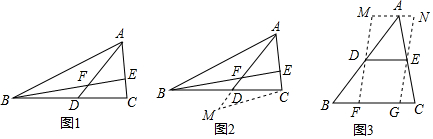
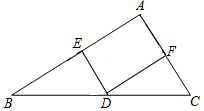 如图,在△ABC中,D,E,F分别是边BC,AB,AC的中点,当∠BAC=90°时,想一想,四边形AEDF是什么特殊的四边形?证明你的结论.
如图,在△ABC中,D,E,F分别是边BC,AB,AC的中点,当∠BAC=90°时,想一想,四边形AEDF是什么特殊的四边形?证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
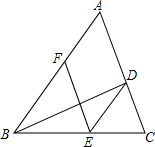 如图,BD是△ABC的角平分线,点E,F分别在边BC,AB上,且DE∥AB,BE=AF.
如图,BD是△ABC的角平分线,点E,F分别在边BC,AB上,且DE∥AB,BE=AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
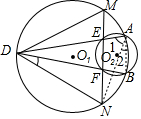 如图,已知⊙O1与⊙O2交于A,B,D为⊙O1上一点,DA,DB交⊙O2于E,F,EF交⊙O1于M,N,求证:DM=DN.(提示:连接AB、AN)
如图,已知⊙O1与⊙O2交于A,B,D为⊙O1上一点,DA,DB交⊙O2于E,F,EF交⊙O1于M,N,求证:DM=DN.(提示:连接AB、AN)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
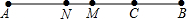 如图,线段AB=8cm,M为线段AB的中点,C为线段MB上一点,且MC=2cm,N为线段AC的中点,则线段MN的长为( )
如图,线段AB=8cm,M为线段AB的中点,C为线段MB上一点,且MC=2cm,N为线段AC的中点,则线段MN的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 苹果品种 | A | B | C | D |
| 单价(元/千克) | 19 | 12.4 | 9 | 7 |
| A. | 一共买了4千克苹果 | B. | (4-x)表示买C品种苹果的千克数 | ||
| C. | 没有买A,D品种的苹果 | D. | 本次购买苹果共支出50元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com