
����Ŀ������������������������Ƴ�����ͼ1��������ķ����˳��й�����ɫ���У�ͼ2��ijƷ��ij�ͺŵ����ij�����Ͷ��ʱ��ʾ��ͼ�����ְ뾶ԼΪ30cm��������BC��ֱ��l����BCE=71�㣬CE=54cm��
��1��������E������ĸ߶ȣ��������ȷ��1cm��
��2�����ݾ��飬������E��CB�ľ�����������������ߣ��ȳ�����0.85ʱ������Ƚ����ʣ�С���Ŀ��Ϊ70cm���ֽ�����E�������������ʸ߶�λ��E������EE���ij����������ȷ��0.1cm��
���ο����ݣ�sin71���0.95��cos71���0.33��tan71���2.90��

���𰸡���1��81cm����2��8.6cm��
��������
��1����EM��BC�ڵ�M����EM=ECsin��BCE�ɵô���
��2����E��H��BC�ڵ�H���ȸ���E��C=![]() ���E��C�ij������ٸ���EE��=CE�䩁CE�ɵô���
���E��C�ij������ٸ���EE��=CE�䩁CE�ɵô���
��1����ͼ1������E��EM��BC�ڵ�M��
������֪��BCE=71�㡢EC=54����EM=ECsin��BCE=54sin71����51.3��������E������ĸ߶�Ϊ51.3+30��81cm��
��2����ͼ2��ʾ������E����E��H��BC�ڵ�H��
������֪E��H=70��0.85=59.5����E��C=![]() =
=![]() ��62.6����EE��=CE�䩁CE=62.6��54=8.6��cm����
��62.6����EE��=CE�䩁CE=62.6��54=8.6��cm����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
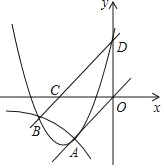
����Ŀ����ͼ����֪�����������ͷ�����������ͼ������A����3����3����
��1���������������ͷ����������ı���ʽ��
��2����ֱ��OA����ƽ�ƺ��뷴����������ͼ���ڵ�B����6��m������x�ύ�ڵ�C����m��ֵ��ֱ��BC�ı���ʽ��
��3���ڣ�2���������£�ֱ��BC��y�ύ�ڵ�D�����Ե�A��B��DΪ����������ε������
��4���ڣ�3���������£���A��B��D�ڶ��κ�����ͼ���ϣ����жϸö��κ����ڵ��������ڵ�ͼ�����Ƿ����һ��E��ʹ�ı���OECD�����S1���ı���OABD�����S���㣺S1=![]() S�������ڣ����E�����ꣻ�������ڣ���˵�����ɣ�
S�������ڣ����E�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������У�Ļ�У�ij��ȤС���������ͼ��ʾ��ֱ��ǽ�ǣ������㹻��������28 m�������Χ��һ�����λ�ABCD�����ֻΧAB��BC���ߣ�����AB=x m������P����һ������ǽCD��AD�ľ���ֱ���15 m��6 m��Ҫ�������Χ�ڻ��ڣ����߽磬���������Ĵ�ϸ���������S�����ֵΪ�� ��

A. 196 B. 195 C. 132 D. 14
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һ�κ���y=mx+4m��2��
��1�������������ͼ��ԭ�㣬��m��ֵ��
��2�������������ͼ���������ޣ���m��ȡֵ��Χ��
��3������mȡ��ʵ�����������ͼ�����㣬���������������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABC�У�AB=AC����ACB=72����

��1����BD��AC��D�����ABD�Ķ�����
��2����CEƽ�֡�ACB����֤��AE=BC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
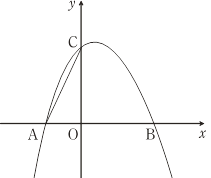
����Ŀ����ͼ�����κ���y=��x2+bx+c��ͼ����x�ύ�ڵ�A(��1��0)��B(2��0)����y���ཻ�ڵ�C��
��1������κ����Ľ���ʽ��
��2������E�ǵ�һ�����������ϵ�һ�����㣬���ı���ABEC��������ʱ�����E�����꣬������ı���ABEC����������
��3������M���������ϣ�����y����Ҳ࣮��M��y�����У��е�ΪD����C��D��MΪ���������������AOC���ƣ���ֱ��д����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������и���
��1��![]()
��2����![]() ��3��2����
��3��2����![]() ��3������
��3������![]() ��3��
��3��
��3��![]()
��4��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�з���һ����OABC����֪��ABC=60�㣬OA=1���ֽ�����OABC��x���������������ת��ÿ�η�ת60�㣬������ת2018�Σ���B���������ΪB1��B2��B3��B4��������B2018������Ϊ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,����ABC��,AC=BC,��ACB=90����D��BC���ӳ����ϣ�����AD����B��BE��AD������ΪE����AC�ڵ�F������CE.
(1)��֤����BCF�ա�ACD.
(2)�����BEC�Ķ�������˵�����ɣ�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com