
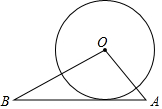
 如图,在△OAB中,OA=2$\sqrt{5}$,OB=4$\sqrt{5}$,OA⊥OB,以O为圆心,4为半径作⊙O,求证:AB是⊙O的切线.
如图,在△OAB中,OA=2$\sqrt{5}$,OB=4$\sqrt{5}$,OA⊥OB,以O为圆心,4为半径作⊙O,求证:AB是⊙O的切线. 分析 作OC⊥AB于C,如图,先利用勾股定理计算出AB=10,再利用面积法求出OC=4,而⊙O的半径为4,则根据切线的判定方法可判断AB是⊙O的切线.
解答 解:作OC⊥AB于C,如图,
∵OA⊥OB,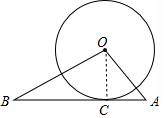
∴∠AOB=90°,
在Rt△OAB中,AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{(2{\sqrt{5}}^{\;})^{2}+(4\sqrt{5})^{2}}$=10,
∵$\frac{1}{2}$OC•AB=$\frac{1}{2}$OB•OA,
∴OC=$\frac{2\sqrt{5}×4\sqrt{5}}{10}$=4,
∵⊙O的半径为4,
∴OC为⊙C的半径,
而OC⊥AB,
∴AB是⊙O的切线.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.在判定一条直线为圆的切线时,当已知条件中未明确指出直线和圆是否有公共点时,常过圆心作该直线的垂线段,证明该线段的长等于半径;当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
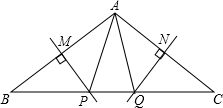 如图所示,MP和 NQ分别垂直平分AB 和AC.
如图所示,MP和 NQ分别垂直平分AB 和AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 当m≠0时,为一元一次方程 | B. | 当m=0时,为一元一次方程 | ||
| C. | 当m=0且n≠0时,为一元一次方程 | D. | 当m=0且n=0时,为一元一次方程 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
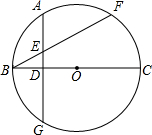 已知:如图,BC为⊙O的直径,BF为弦,A为$\widehat{BF}$的中点,AD⊥BC,垂足为D,AD和BF相交于点E,求证:AE=BE.
已知:如图,BC为⊙O的直径,BF为弦,A为$\widehat{BF}$的中点,AD⊥BC,垂足为D,AD和BF相交于点E,求证:AE=BE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com