
【题目】如图,已知直线AB和CD相交于点O,射线OE⊥AB于点O,射线OF⊥CD于点O,且∠AOF=25°.求∠BOC与∠EOF的度数.

【答案】∠BOC=115°, ∠EOF=65°
【解析】
由OF⊥CD,得∠FOD=90°,已知∠AOF=25°,从而由平角的性质可求得∠AOC的度数,然后由邻补角的性质可知∠BOC的度数,由OE⊥AB,∠AOE=90°,可得∠FOE=∠AOE-∠AOF.
因为OF⊥CD,所以∠DOF=90°.
因为∠AOC+∠AOF+∠DOF=180°,
∠AOF=25°,所以∠AOC=65°.
因为∠AOC+∠BOC=180°,
所以∠BOC=115°;
因为OE⊥AB,所以∠AOE=90°,
所以∠AOF+∠EOF=90°.
因为∠AOF=25°,所以∠EOF=65°.
故答案为:∠BOC=115°; ∠EOF=65°.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.∠BAD=60°,AC平分∠BAD,AC=2,BN的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ,
,![]() .试说明直线
.试说明直线![]() 与
与![]() 垂直.(请在下面的解答过程的空格内填空或在括号内填写理由).
垂直.(请在下面的解答过程的空格内填空或在括号内填写理由).

理由:![]() ,(已知)
,(已知)
![]()
![]() ,
,![]()
![]()
![]() .
.![]()
![]()
又![]() ,(已知)
,(已知)
![]()
![]() .(等量代换)
.(等量代换)
![]()
![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]() ,(已知)
,(已知)
![]() ,
,![]() ,
,
![]()
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是某学校的平面图的一部分,其中A代表音乐楼,B代表实验楼,C代表图书馆,正方形网格中每个小正方形的边长为1,试结合图形回答下列问题:
(1)用(1,4)表示音乐楼A的位置,那么实验楼B和图书馆C的位置如何表示?
(2)三座楼房之间修三条路AC,AB,BC,且已知这三条路的长度存在下列关系:AC2+AB2=BC2.量得B到A的距离为3![]() ,若记东偏北方向为“+”,东偏南方向为“-”,则B点相对于A点的位置记作(-45°,3
,若记东偏北方向为“+”,东偏南方向为“-”,则B点相对于A点的位置记作(-45°,3![]() ).那么,C点相对于A点的位置可如何表示?
).那么,C点相对于A点的位置可如何表示?
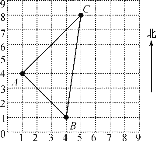
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数p,q,我们用符号min{p,q}表示p,q两数中较小的数,如min{1,2}=1,因此,min{﹣ ![]() ,﹣
,﹣ ![]() }=;若min{(x﹣1)2 , x2}=1,则x= .
}=;若min{(x﹣1)2 , x2}=1,则x= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在直线形的公路上由A向B行驶,M、N分别是位于公路AB两侧的两个学校,如图.

(1)汽车行驶时,会对公路两旁的学校都造成一定的影响,当汽车行驶到何处时,分别对两个学校影响最大?在图中标出来;
(2)当汽车从A向B行驶时,在哪一段上对两个学校影响越来越大?越来越小?对M学校影响逐渐减小而对N学校影响逐渐增大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个二次函数图象的顶点相同,开口大小相同,但开口方向相反,则称这两个二次函数为“对称二次函数”.
(1)请写出二次函数y=2(x﹣2)2+1的“对称二次函数”;
(2)已知关于x的二次函数y1=x2﹣3x+1和y2=ax2+bx+c,若y1﹣y2与y1互为“对称二次函数”,求函数y2的表达式,并求出当﹣3≤x≤3时,y2的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,O是等边△ABC内一点,连接OA、OB、OC,且OA=3,OB=4,OC=5,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.求:

①旋转角的度数;
②线段OD的长;
③∠BDC的度数.
(2)如图2所示,O是等腰直角△ABC(∠ABC=90°)内一点,连接OA、OB、OC,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.当OA、OB、OC满足什么条件时,∠ODC=90°?请给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com