
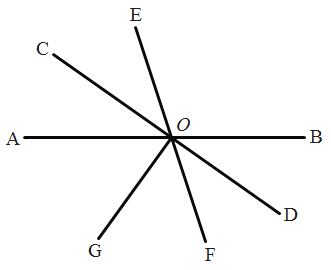
【题目】如图,已知直线![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的度数;
的度数;
(2)若![]() 是
是![]() 的平分线,那么
的平分线,那么![]() 是
是![]() 的平分线吗?说明你的理由.
的平分线吗?说明你的理由.
【答案】(1)∠AOG =54°;(2) OC是∠AOE的平分线,理由见解析.
【解析】
(1)根据A,O,B在同一直线即可求出∠AOG的度数;
(2)根据OG平分∠AOF知,∠AOF的度数,再由OG⊥CD,得∠COG=90°,即可求出∠AOE与∠AOC的度数,即可进行求证.
(1)由OG⊥CD,得∠DOG=90°,
∴∠AOG=180°-∠DOG-∠BOD=54°;
(2) OC是∠AOE的平分线,理由如下.
∵OG平分∠AOF,
∴∠AOF=2∠AOG=108°,
则∠AOE=180°-∠AOF=72°,
又∵OG⊥CD,
∴∠COG=90°,
∴∠AOC=90°-∠AOG=36°,
故∠AOE=2∠AOC,
故OC是∠AOE的平分线.


科目:初中数学 来源: 题型:
【题目】垃圾对环境的影响日益严重,垃圾危机的警钟被再次拉响.我市某中学积极响应国家号召,落实垃圾“分类回收,科学处理”的政策,准备购买![]() 、
、![]() 两种型号的垃圾分类回收箱共20只,放在校园各个合适位置,以方便师生进行垃圾分类投放.若购买
两种型号的垃圾分类回收箱共20只,放在校园各个合适位置,以方便师生进行垃圾分类投放.若购买![]() 型14只、
型14只、![]() 型6只,共需4240元;若购买
型6只,共需4240元;若购买![]() 型8只、
型8只、![]() 型12只,共需4480元.求
型12只,共需4480元.求![]() 型、
型、![]() 型垃圾分类回收箱的单价.
型垃圾分类回收箱的单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E,F分别是锐角∠A两边上的点,AE=AF,分别以点E,F为圆心,以AE的长为半径画弧,两弧相交于点D,连接DE,DF.
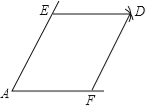
(1)请你判断所画四边形的性状,并说明理由;
(2)连接EF,若AE=8厘米,∠A=60°,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则CE的长为___________.
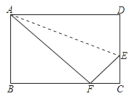
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组从![]() 地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:
地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:![]() )
)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
(1)在第__________次记录时距![]() 地最远;
地最远;
(2)求收工时距![]() 地多远?
地多远?
(3)若每千米耗油![]() 升,每升汽油需
升,每升汽油需![]() 元,问检修小组工作一天需汽油费多少元?
元,问检修小组工作一天需汽油费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上A、B两点对应的数分别为﹣2和8,P为数轴上任意一点且对应的数为x,C为线段PA的中点.
(1)若点P在线段AB上,求2BC﹣BP的值;
(2)若点P在线段AB的延长线上,式子2BC﹣BP的值是定值吗?若是,求出它的值,若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com