
【题目】如图,在△ABC中,AB=AC=8,BC=12,点D从B出发以每秒2个单位的速度在线段BC上从过点B向点C运动,点E同时从点C出发,以每秒2个单位的速度在线段AC上从点A运动,连接AD、DE,设D、E两点运动时间为![]() 秒.
秒.
(1)运动_____秒时,CD=3AE.
(2)运动多少秒时,△ABD≌△DCE能成立,并说明理由;
(3)若△ABD≌△DCE,∠BAC=![]() 则∠ADE=_______(用含
则∠ADE=_______(用含![]() 的式子表示)。
的式子表示)。

【答案】(1)3秒;(2)当t=2时,△ABD与△DCE全等;理由见解析;(3)90°-0.5ɑ.
【解析】
(1)依据BD=CE=2t,可得CD=12-2t,AE=8-2t,再根据当DC=3AE时,12-2t =3(8-2t),可得t的值;
(2)当△ABD≌△DCE成立时,AB=CD=8,根据12-2t=8,可得t的值;
(3)依据∠CDE=∠BAD,∠ADE=180°-∠CDE-∠ADB,∠B=∠180°-∠BAD-∠ADB,即可得到∠ADE=∠B,再根据∠BAC=α,AB=AC,即可得出∠ADE.
(1)由题可得,BD=CE=2t,
∴CD=12-2t,AE=8-2t,
∴当DC=3AE时,12-2t =3(8-2t),
解得t=3,
故答案为:3;
(2)当△ABD≌△DCE成立时,AB=CD=8,
∴12-2t=8,
解得t=2,
∴运动2秒时,△ABD≌△DCE能成立;
(3)当△ABD≌△DCE时,∠CDE=∠BAD,
又∵∠ADE=180°-∠CDE-∠ADB,∠B=∠180°-∠BAD-∠ADB,
∴∠ADE=∠B,
又∵∠BAC=α,AB=AC,
∴∠ADE=∠B=![]() (180°-α)=90°-
(180°-α)=90°-![]() α.
α.
故答案为:90°-![]() α.
α.


科目:初中数学 来源: 题型:
【题目】如图,B、D、E、F是直线 l上四点,在直线 l的同侧作△ABE和△CDF,且 AB∥CD,∠A=40°.作BG⊥AE于 G,FH⊥CD于 H,BG与 FH交于 P点.
(1)如图 1,B、E、D、F从左至右顺次排列,∠ABD=90°,求∠GPH;
(2)如图 2,B、E、D、F从左至右顺次排列,△ABE与△CDF均为锐角三角形,求∠GPH;
(3)如图 3,F、B、E、D从左至右顺次排列,△ABE为锐角三角形,△CDF为钝角三角形,则∠GPH的度 数为多少?请画出图形并直接写出结果,不需证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F、H分别是AB、BC、CD的中点,CE、DF交于G,连接AG、HG.下列结论:①CE⊥DF;②AG=DG;③∠CHG=∠DAG;④2HG=AD.正确的有( )
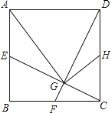
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
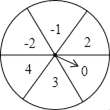
【题目】如图是一个平均被分成6等分的圆,每一个扇形中都标有相应的数字,甲乙两人分别转动转盘,设甲转动转盘后指针所指区域内的数字为x,乙转动转盘后指针所指区域内的数字为y(当指针在边界上时,重转一次,直到指向一个区域为止).
(1)直接写出甲转动转盘后所指区域内的数字为负数的概率;
(2)用树状图或列表法,求出点(x,y)落在第二象限内的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
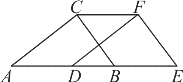
【题目】如图,在直角三角形ABC中,∠ACB=90°,AC=4cm,BC=3cm,将三角形ABC沿AB方向向右平移得到三角形DEF,若AE=8cm,DB=2cm.
(1)求三角形ABC向右平移的距离AD的长;
(2)求四边形AEFC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,同时将点A(﹣1,0)、B(3,0)向上平移2个单位长度再向右平移1个单位长度,分别得到A、B的对应点C、D.连接AC,BD

(1)求点C、D的坐标,并描出A、B、C、D点,求四边形ABDC面积;
(2)在坐标轴上是否存在点P,连接PA、PC使S△PAC=S四边形ABCD?若存在,求点P坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,点E是线段BO上的一个动点(可以与O、B重合),点F为射线DC上一点,若∠ABC=60,∠AEF=120,AB=5,则EF的取值范围是_____.
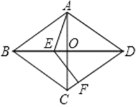
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】媒体报道,近期“手足口病”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“手足口病”,对教室进行“薰药消毒”.已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所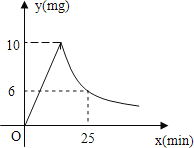
示(即图中线段OA和双曲线在A点及其右侧的部分),根据图象所示信息,解答下列问题:
(1)写出从药物释放开始,y与x之间的函数关系式及自变量的取值范围;
(2)据测定,当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始,至少在多长时间内,师生不能进入教室?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com