
【题目】如图所示,直线y=x+b与双曲线y=![]() (x<0)交于点A(﹣1,﹣5),并分别与x轴、y轴交于点C、B.
(x<0)交于点A(﹣1,﹣5),并分别与x轴、y轴交于点C、B.
(1)求出b、m的值;
(2)点D在x轴的正半轴上,若以点D、C、B组成的三角形与△OAB相似,试求点D的坐标.

【答案】(1)b=﹣4,m=5;(2)D点坐标为:(6,0),(20,0).
【解析】试题分析:(1)将A坐标代入y=x+b,求出b的值,将点A的坐标代入双曲线解析式中,求出m的值即可;(2)如图所示,过点A作AE⊥y轴于点E,根据已知条件易得∠BCD=∠ABO=135°,再求得AB=![]() ,BO=4,BC=4
,BO=4,BC=4![]() ,分△AOB∽BD′C和△AOB∽DBC两种情况求点D的坐标即可.
,分△AOB∽BD′C和△AOB∽DBC两种情况求点D的坐标即可.
试题解析:
(1)∵直线y=x+b的双曲线y=![]() 交于点A(﹣1,﹣5),
交于点A(﹣1,﹣5),
∴﹣1+b=﹣5,m=(﹣1)×(﹣5)=5,
∴解得:b=﹣4,m=5;
(2)如图所示:过点A作AE⊥y轴于点E,
∵CO=OB=4,∠COB=90°,
∴∠OBC=∠OCB=45°,
∴∠ABE=45°,∠BCD=135°,
∴∠ABO=135°,
∵AB=![]() =
=![]() ,BO=4,BC=4
,BO=4,BC=4![]() ,
,
当△AOB∽DBC时,![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得:CD=2,
∴DO=6,
∴D点坐标为:(6,0);
当△AOB∽BD′C时,![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得:CD′=16,
∴D′O=16+4=20,
∴D′点坐标为:(20,0),
综上所述,符合要求的D点坐标为:(6,0),(20,0).



科目:初中数学 来源: 题型:
【题目】已知线段AB,点C在直线AB上,D为线段BC的中点.
(1)若AB=8 ,AC=2,求线段CD的长.
![]()
(2)若点E是线段AC的中点,直接写出线段DE和AB的数量关系是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.

查看答案和解析>>
科目:初中数学 来源: 题型:
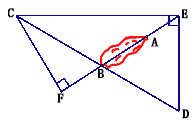
【题目】海上有一小岛,为了测量小岛两端A、B的距离,测量人员设计了一种测量方法,如图所示,已知B点是CD的中点,E是BA延长线上的一点,测得AE=10海里,DE=30海里,且DE⊥EC,cos∠D=![]() .
.
(1)求小岛两端A、B的距离;
(2)过点C作CF⊥AB交AB的延长线于点F,求sin∠BCF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,矩形OABC放置于平面直角坐标系中,点O与原点重合,点A在x轴正半轴上,点C在y轴正半轴上,点B的坐标为(6,3),点D是边BC上的一动点,连接OD,作点C关于直线OD的对称点C′.
(1)若点C、C′、A在一直线上时,求点D的坐标;
(2)若点C′到矩形两对边所在直线距离之比为1:2时,求点C′的坐标;
(3)若连接BC′,则线段BC′的长度范围是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国庆节社会实践活动中,盐城某校甲、乙、丙三位同学一起调查了高峰时段盐靖高速、盐洛高速和沈海高速的车流量(每小时通过观测点的汽车车辆数),三位同学汇报高峰时段的车流量情况如下:
甲同学说:“盐靖高速车流量为每小时2000辆.”
乙同学说:“沈海高速的车流量比盐洛高速的车流量每小时多400辆.”
丙同学说:“盐洛高速车流量的5倍与沈海高速车流量的差是盐靖高速车流量的2倍.”
请你根据他们所提供的信息,求出高峰时段盐洛高速和沈海高速的车流量分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某苹果生产基地,用30名工人进行采摘或加工苹果,每名工人只能做其中一项工作.苹果的销售方式有两种:一种是可以直接出售,另一种是可以将采摘的苹果加工成罐头出售.直接出售每吨获利4 000元,加工成罐头出售每吨获利10 000元.采摘的工人每人可以采摘苹果0.4吨,加工罐头的工人每人可加工苹果0.3吨.采摘的苹果一部分用于加工罐头,其余直接出售.设有x名工人进行苹果采摘,罐头和苹果全部售出后,总利润为y元.
(1)加工成罐头的苹果数量为 吨,直接出售的苹果数量为 吨.(用含x的代数式表示)
(2)求y与x之间的函数关系式,并求出自变量的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com