练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．为落实国务院房地产调控政策，使“居者有其屋”，某市加快了廉租房的建设力度，2013年市政府共投资2亿元人民币建设了廉租房8万平方米，预计到2015年底三年共累计投资9.5亿元人民币建设廉租房，若在这两年内投资的增长率相同．
    （1）求每年市政府投资的增长率；
    （2）求2015年政府共投资多少亿元建设廉租房．

    分析 （1）首先设每年市政府投资的增长率为x．则2014年投资2（1+x）亿元，2015年投资2（1+x）2亿元，根据到2015年底三年共累计投资9.5亿元人民币建设廉租房，列方程求解．
    （2）根据（1）中的x的值代入2（1+x）2计算即可．

    解答 解：（1）设每年市政府投资的增长率为x，根据题意，得：
    2+2（1+x）+2（1+x）2=9.5，
    整理，得：x2+3x-1.75=0，
    解得：x1=0.5，x2=-3.5（舍去）．
    答：每年市政府投资的增长率为50%．

    （2）2（1+50%）2=4.5（亿元），
    答：2015年政府共投资4.5亿元建设廉租房．

    点评 此题主要考查了一元二次方程的实际应用，解题的关键是掌握增长率问题中的一般公式为a（1+x）n，其中n为共增长了几年，a为第一年的原始数据，x是增长率．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    7．如图，已知等边△ABC的边长为10，点P在BC边上，且BP=2，试判断以P为圆心BP为半径的圆与以AC为直径的圆O的位置关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

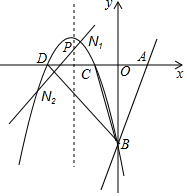    8．如图所示，直线l：y=3x-3与x轴交于点A，与y轴交于点B，把△AOB沿y轴翻折，点A落到点C，抛物线过点B，C和D（-3，0）．
    （1）求直线BD和抛物线的解析式；
    （2）若点M是抛物线上一动点，是否存在这样的点M使△BDM是以BD为直角边的直角三角形，若存在，求出点M的坐标；若不存在，请说明理由；
    （3）若点P（-2，$\frac{3}{4}$）是对称轴上一点，过点P的任意一条与y轴不平行的直线与抛物线交于两点N1，N2，说明$\frac{{N}_{1}P•{N}_{2}P}{{N}_{1}{N}_{2}}$是否是定值？若是定值，请求出这个定值，若不是，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，在△ABC中，∠ACB=90°，AC=BC，E为AC边的中点，过点A作AD⊥AB交BE的延长线于点D，CG平分∠ACB交BD于点G，F为AB边上一点，连接CF，且∠ACF=∠CBG．
    （1）证明：AF=CG；
    （2）判断点C在BD上的位置，并说明理由；
    （3）在（2）的条件下，若DE=3，求CF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

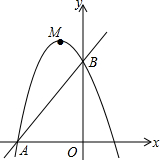    12．如图，在平面直角坐标系xOy中，直线y=x+3与坐标轴分别交于A，B两点，过A、B两点的抛物线为y=-x2+bx+c．
    （1）求抛物线的解析式
    （2）直接写出该抛物线顶点M的坐标，求出线段MB的长度．
    （3）若P（x，y）是该抛物线上的一个动点，是否存在这样的点P，使得它到线段AB两端的距离相等，即使得PA=PB，若存在，试求出所有符合条件的点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．设S1=13，S2=13+23，S3=13+23+33，S4=13+23+33+43．
    （1）写出S5，并求出S5的值；
    （2）用含有n的代数式表示Sn；
    （3）计算：$\sqrt{{S}_{1}}$+$\sqrt{{S}_{2}}$+$\sqrt{{S}_{3}}$+…+$\sqrt{{S}_{10}}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，延长Rt△ABC斜边AB至D点，使BD=AB，连结CD，若cot∠BCD=2，求tanA的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．我们用[a]表示不大于a的最大整数，例如：[3.5]=3，[4]=4，[-1.5]=-2；用{a}表示大于a的最小整数，例如：{3.5}=4，{1}=2，{-2.5}=-2．解决下列问题：
    （1）[-5.5]=-6，{2.5}=3．
    （2）若[x]=3，则x的取值范围是3≤x＜4；若{y}=-2，则y的取值范围是-3≤y＜-2．
    （3）已知x，y满足方程组$\left\{\begin{array}{l}{[x]+3\{y\}=2}\\{[x]-4\{y\}=-5}\end{array}\right.$，求x，y的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．鸡冠区西郊乡前年的人均收入为12000元，今年的人均收入为14520元，求人均收入的年平均增长率是多少？

    查看答案和解析>>

    同步练习册答案