
【题目】如图1,△ABC中,AD为BC边上的的中线,则S△ABD= S△ADC.

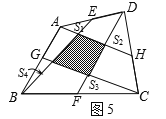
实践探究
(1)在图2中,E、F分别为矩形ABCD的边AD、BC的中点,则S阴和S矩形ABCD之间满足的关系式为 ;
(2)在图3中,E、F分别为平行四边形ABCD的边AD、BC的中点,则S阴和S平行四边形ABCD之间满足的关系式为 ;
(3)在图4中,E、F分别为任意四边形ABCD的边AD、BC的中点,则S阴和S四边形ABCD之间满足的关系式为 ;
解决问题:
(4)在图5中,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,并且图中阴影部分的面积为20平方米,求图中四个小三角形的面积和是多少?即求S1+ S2+ S3+ S4=?
【答案】(1)S阴=![]() S矩形ABCD;(2)S阴=
S矩形ABCD;(2)S阴=![]() S平行四边形ABCD;(3)S阴=
S平行四边形ABCD;(3)S阴=![]() S四边形ABCD;(4)20.
S四边形ABCD;(4)20.
【解析】
试题分析:(1)利用E、F分别为矩形ABCD的边AD、BC的中点,分别求得S阴和S矩形ABCD即可.
(2)利用E、F分别为平行四边形ABCD的边AD、BC的中点,分别求则S阴和S平行四边形ABCD即可.
(3)利用E、F分别为任意四边形ABCD的边AD、BC的中点,分别求得则S阴和S四边形ABCD即可.
(4)先设空白处面积分别为:x、y、m、n由上得S四边形BEDF=![]() S四边形ABCD,S四边形AHCG=
S四边形ABCD,S四边形AHCG=![]() S四边形ABCD,分别求得S1、S2、S3、S4.然后S1+S2+S3+S4=S阴即可.
S四边形ABCD,分别求得S1、S2、S3、S4.然后S1+S2+S3+S4=S阴即可.
试题解析:(1)由E、F分别为矩形ABCD的边AD、BC的中点,
得S阴=BF![]() CD=
CD=![]() BC
BC![]() CD,
CD,
S矩形ABCD=BC![]() CD,
CD,
所以S阴=![]() S矩形ABCD;
S矩形ABCD;
(2)同理可得;S阴=![]() S平行四边形ABCD;
S平行四边形ABCD;
(3)同理可得;S阴=![]() S四边形ABCD;
S四边形ABCD;
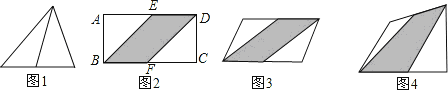
(4)设空白处面积分别为:x、y、m、n(见下图),
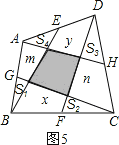
由上得S四边形BEDF=![]() S四边形ABCD,S四边形AHCG=
S四边形ABCD,S四边形AHCG=![]() S四边形ABCD,
S四边形ABCD,
∴S1+x+S2+S3+y+S4=![]() S四边形ABCD.S1+m+S4+S2+n+S3=
S四边形ABCD.S1+m+S4+S2+n+S3=![]() S四边形ABCD,
S四边形ABCD,
∴(S1+x+S2+S3+y+S4)+(S1+m+S4+S2+n+S3)=S四边形ABCD.
∴(S1+x+S2+S3+y+S4)+(S1+m+S4+S2+n+S3)=S1+x+S2+n+S3+y+S4+m+S阴
∴S1+S2+S3+S4=S阴=20.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】作图题(不写作法,保留作图痕迹):
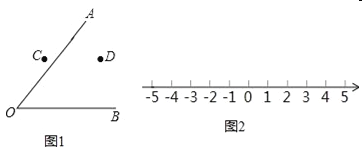
(1)尺规作图:校园有两条路OA、OB,在交叉路口附近有两块宣传牌C、D,学校准备在这里安装一盏路灯,要求灯柱的位置P离两块宣传牌一样远,并且到两条路的距离也一样远,请你帮助画出灯柱的位置P(如图1).(不写画图过程,保留作图痕迹)
(2)用直尺和圆规在如图2所示的数轴上作出表示![]() 的点.
的点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要得到y=﹣2(x+2)2﹣3的图象,需将抛物线y=﹣2x2作如下平移( )
A. 向右平移2个单位,再向上平移3个单位
B. 向右平移2个单位,再向下平移3个单位
C. 向左平移2个单位,再向上平移3个单位
D. 向左平移2个单位,再向下平移3个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
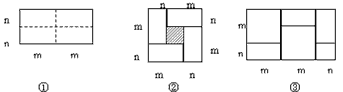
【题目】图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
(1)图②中的阴影部分的正方形边长为 ;
(2)观察图②,三个代数式![]() 之间的等量关系是
之间的等量关系是
;
(3)观察图③,你能得到怎样的代数恒等式呢?;
(4)试画出一个几何图形,使它的面积能表示![]() .(画在虚线框内)
.(画在虚线框内)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明为了通过描点法作出函数y=x2-x+1的图象,先取自变量x的7个值满足:x2-x1=x3-x2=…=x7-x6=d,再分别算出对应的y值,列出表:

记m1=y2-y1,m2=y3-y2,m3=y4-y3,m4=y5-y4,…;s1=m2-m1,s2=m3-m2,s3=m4-m3,…
(1)判断s1、s2、s3之间关系,并说明理由;
(2)若将函数“y=x2-x+1”改为“y=ax2+bx+c(a≠0)”,列出表:

其他条件不变,判断s1、s2、s3之间关系,并说明理由;
(3)小明为了通过描点法作出函数y=ax2+bx+c(a≠0)的图象,列出表:

由于小明的粗心,表中有一个y值算错了,请指出算错的y值(直接写答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程 x2﹣3x+5=0的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 只有一个实数根 D. 没有实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,DF⊥AC于F.
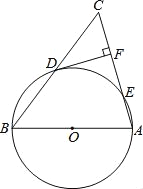
(1)求证:DF为⊙O的切线;
(2)若cosC=![]() ,CF=9,求AE的长.
,CF=9,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com