Question

19．在平面直角坐标系中，O为坐标原点，直线y=-x+6与x轴交于点A，与y轴交于点B，抛物线y=ax²-6ax过线O、A交直线AB于点C，且C点的纵坐标比横坐标大4．
（1）如图1，求a的值；
（2）如图2，动点D在线段OB上，点E在线段AB上，DE∥x，点F在线段DC的延长线上，EF∥y轴，交x轴于点G，当点F恰好落在抛物线上时，求点D、F的坐标；
（3）在（2）的条件下，点P在第一象限内的抛物线上，PH⊥CD于点H，若tan$∠FPH=\frac{3}{4}$，求点P的坐标．

Answer 1

分析 （1）先由点C的坐标特点，求出点C坐标，点C坐标代入抛物线解析式中求出a，
（2）设出点D坐标，表示出CD解析式，表示出点E，F坐标，把点F的坐标代入抛物线解析式中，即可；
（3）先判断出△FKD≌△DOA，得出AD=DF，再求出∠ADF，得到三角形ADF是等腰直角三角形，再由垂直平分线判断出AQ=OQ，进而判断出PN=$\frac{2}{3}$MN，设出点P坐标，确定出PH解析式，利用PN=$\frac{2}{3}$MN，建立方程求解即可．

解答 解：设C（x，-x+6），
∵C点的纵坐标比横坐标大4，
∴x+4=-x+6，
∴x=1，
∴C（1，5），
∵点C在抛物线y=ax²-6ax上，
∴a-6a=5，
∴a=-1，
（2）设D（0．m）
∵C（1，5），
∴直线CD解析式为y=（5-m）x+m，
∵DE∥x轴，
∴E的纵坐标为m，
∵点E在y=-x+6上，
∴E（6-m，m）
∴点F的横坐标为6-m，
∵点F在直线CD解析式为y=（5-m）x+m上，
∴F（6-m，m²-10m+30），
由（1）得，抛物线解析式为y=-x²+6x，
∴m²-10m+30=-（6-m）²+6（6-m），
∴m=5（舍）或m=3，
∴D（0，3），F（3，9），
（3）如图，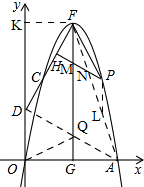

过点F作FK⊥y轴，连接AD，AF，AF交PH于N，PH交PG于M，过点P作PL⊥y轴交AF于L，
∵F（3，9），D（0，3），A（6，0），
∴FK=OD=3，DK=OA=6，
∵∠FKD=∠DOA=90°，
∴△FKD≌△DOA，
∴∠DFK=∠ADO，AD=DF，
∵∠DFK+∠KDF=90°，
∴∠ADO+∠HDF=90°，
∴∠ADF=180°-90°=90°，
∴△ADF是等腰直角三角形，
∵PH⊥CD，
∴PH∥AD，
∴∠AFD=45°，
设AD交FG于Q，
∵G（3，0），A（6，0），
∴OG=AG，
∵FG∥y轴，
∴AQ=OQ，
∵PH∥AD，
∴$\frac{HM}{DQ}=\frac{FM}{FQ}=\frac{MN}{AQ}$，
∴HM=MN，
∵∠AFD=45°，
∴CF=HN，
∵tan∠FPH=$\frac{HF}{HP}=\frac{3}{4}$，
∴PN=$\frac{2}{3}$MN，
∵PL∥FH，
∴$\frac{PL}{PM}=\frac{PN}{MN}=\frac{2}{3}$，
∵F（3，9），A（6，0），D（0，3），
∴直线AD解析式为y=-$\frac{1}{2}$x+3，
直线AF解析式为y=-3x+18，
设P（t，-t²+6t），
∴直线PH解析式为y=-$\frac{1}{2}$x-t²+$\frac{13}{2}$t，
∴M（3，-t²+$\frac{13}{2}$t-$\frac{3}{2}$），
∴FM=9-（-t²+$\frac{13}{2}$t-$\frac{3}{2}$）=t²-$\frac{13}{2}$t+$\frac{21}{2}$，
∵PL=-t²+9t-18，
∴3（-t²+9t-18）=2（t²-$\frac{13}{2}$t+$\frac{21}{2}$），
∴t=3（舍）或t=5，
∴P（5，5）．

点评 此题是二次函数综合题，主要考查了待定系数法求函数解析式，三角形全等的判定和性质，等腰直角三角形的判定和性质，平行线分线段成比例定理，解本题的关键是用待定系数法求函数解析式（如：直线CD解析式为y=（5-m）x+m，直线AD解析式为y=-$\frac{1}{2}$x+3，直线AF解析式为y=-3x+18），用方程的思想解决问题是本题的难点．