
分析 首先化简(2x+y)2-(x-2y)(-2y-x)+(-3x2y)÷($\frac{3}{5}$x2y-1),然后把x=$\frac{1}{5}$,y=-$\frac{1}{2}$代入化简后的算式,求出算式的值是多少即可.
解答 解:(2x+y)2-(x-2y)(-2y-x)+(-3x2y)÷($\frac{3}{5}$x2y-1)
=4x2+4xy+y2+x2-4y2-5y2
=5x2+4xy-8y2
当x=$\frac{1}{5}$,y=-$\frac{1}{2}$时,
原式=5×${(\frac{1}{5})}^{2}$+4×$\frac{1}{5}$×(-$\frac{1}{2}$)-8×${(-\frac{1}{2})}^{2}$
=$\frac{1}{5}$-$\frac{2}{5}$-2
=-2$\frac{1}{5}$
点评 此题主要考查了整式的混合运算-化简求值,要熟练掌握,注意先按运算顺序把整式化简,再把对应字母的值代入求整式的值.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
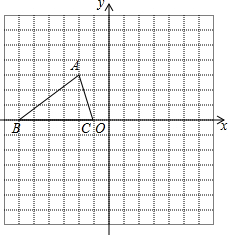 如图,已知△ABC的三个顶点坐标为A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC的三个顶点坐标为A(-2,3)、B(-6,0)、C(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com