
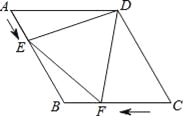
【题目】如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为 .
【答案】![]()
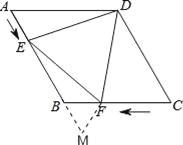
【解析】试题分析:延长AB至M,使BM=AE,连接FM,证出△DAE≌EMF,得到△BMF是等边三角形,再利用菱形的边长为4求出时间t的值.延长AB至M,使BM=AE,连接FM, ∵四边形ABCD是菱形,∠ADC=120°
∴AB=AD,∠A=60°, ∵BM=AE, ∴AD=ME, ∵△DEF为等边三角形,
∴∠DAE=∠DFE=60°,DE=EF=FD, ∴∠MEF+∠DEA═120°,∠ADE+∠DEA=180°﹣∠A=120°,
∴∠MEF=∠ADE, ∴△DAE≌EMF(SAS),∴AE=MF,∠M=∠A=60°, 又∵BM=AE,
∴△BMF是等边三角形, ∴BF=AE, ∵AE=t,CF=2t, ∴BC=CF+BF=2t+t=3t, ∵BC=4,
∴3t=4, ∴t=![]()


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 斜边相等的两个直角三角形全等 B. 腰相等的两个等腰三角形全等
C. 有一边相等的等腰直角三角形全等 D. 有一边相等的两个等边三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,动点A(a,0)在x轴的正半轴上,定点B(m, n)在第一象限内(m<2≤a).在△OAB外作正方形ABCD和正方形OBEF , 连接FD , 点M为线段FD的中点.作BB1⊥x轴于点B1 , 作FF1⊥x轴于点F1.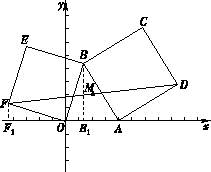
(1)填空:由△≌△ , 及B(m, n)可得点F的坐标为 , 同理可得点D的坐标为;(说明:点F , 点D的坐标用含m , n , a的式子表示)
(2)直接利用(1)的结论解决下列问题:
①当点A在x轴的正半轴上指定范围内运动时,点M总落在一个函数图象上,求该函数的解析式(不必写出自变量x的取值范围);
②当点A在x轴的正半轴上运动且满足2≤a≤8时,求点M所经过的路径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
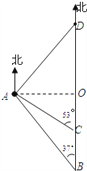
【题目】如图,一艘货船以每小时48海里的速度从港口B出发,沿正北方向航行.在港口B处时,测得灯塔A处在B处的北偏西37°方向上,航行至C处,测得A处在C处的北偏西53°方向上,且A、C之间的距离是45海里.在货船航行的过程中,求货船与灯塔A之间的最短距离及B、C之间的距离;若货船从港口B出发2小时后到达D,求A、D之间的距离.
(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a、b、c为平面上三条不同直线,
(1)若a∥b,b∥c,则a与c的位置关系是________;
(2)若a⊥b,b⊥c,则a与c的位置关系是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
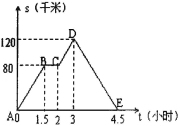
【题目】如图中的图像(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;②汽车在行驶途中停留了0.5小时;③汽车在整个行驶过程中的平均速度为80.8千米/时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减小.⑤汽车离出发地64千米是在汽车出发后1.2小时时。其中正确的说法共有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE;

(1)求证:△ACD≌△BCE;
(2)若∠D=50°,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校初一某班学生的平均体重是45公斤.
(1)下表给出了该班6位同学的体重情况(单位:公斤),完成下表
姓 名 | 小丽 | 小华 | 小明 | 小方 | 小颖 | 小宝 |
体 重 | 37 | 50 | 40 |
| 36 | 48 |
体重与平均体重的差值 | ﹣8 | +5 |
| +2 |
|
|
(2)最重的与最轻的同学的体重相差多少?
(3)这6位同学的平均体重是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com