
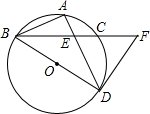
已知:如图,BD为⊙O的直径,AB=AC,AD交BC于E,AE=2,ED=4.
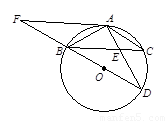
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使BF=OB,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
(1)证明∠ABC=∠D, ∠BAE=∠DAB可得△ABE∽△ADB (2)2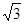
(3)证明△FAO是Rt△,即OA⊥FA,所以直线FA与⊙O相切
【解析】
试题分析:(1)证明:∵AB=AC,
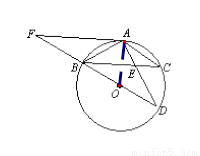
∴∠ABC=∠C,
∵∠C=∠D,
∴∠ABC=∠D,
又∵∠BAE=∠DAB,
∴△ABE∽△ADB
(2)解:∵△ABE∽△ADB,
∴
∴AB2=AD?AE=(AE+ED)?AE=(2+4)×2=12,
∴AB=2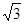
(3)解:直线FA与⊙O相切
理由如下:连接OA
∵ BD是⊙O的直径
∴∠BAD=90°
在Rt△BAD中,AD= AE+ED=2+4=6,由(2)得AB=2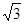
∴有BD=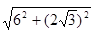 =
=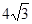
∴OB=OD=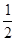 BD=2
BD=2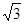
∴BF=OB= 2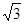
在△FAO中,BF=OB=AB=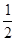 FO=
2
FO=
2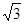
∴△FAO是Rt△,即OA⊥FA
∴直线FA与⊙O相切
考点:
点评:直线与圆相切,相似三角形
点评:本题考查直线与圆相切,平行四边形,掌握直线与圆相切的概念和性质,并能判断直线与圆相切,掌握相似三角形的判定方法,会判定两个三角形相似


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 点E,AE=2,ED=4.
点E,AE=2,ED=4.查看答案和解析>>
科目:初中数学 来源: 题型:
 23、已知:如图,BD为平行四边形ABCD的对角线,O为BD的中点,EF⊥BD于点O,与AD,BC分别交于点E,F.
23、已知:如图,BD为平行四边形ABCD的对角线,O为BD的中点,EF⊥BD于点O,与AD,BC分别交于点E,F.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,BD为⊙O的直径,点A是劣弧BC的中点,AD交BC于点E,连接AB.
已知:如图,BD为⊙O的直径,点A是劣弧BC的中点,AD交BC于点E,连接AB.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知,如图,BD为平行四边形ABCD的对角线,O为BD的中点,EF⊥BD于点O,与AD、BC分别交于点E、F.试判断四边形BFDE的形状,并证明你的结论.
已知,如图,BD为平行四边形ABCD的对角线,O为BD的中点,EF⊥BD于点O,与AD、BC分别交于点E、F.试判断四边形BFDE的形状,并证明你的结论.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com