
【题目】如图,在正方形ABCD中,对角线AC,BD交于点0,过点0的直线分别交边AD,BC于点E,F,EF=6.则AE2+BF2的值为( )
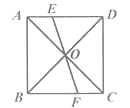
A. 9 B. 16 C. 18 D. 36
【答案】C
【解析】过点A作AM∥EF交BC于点M,易证四边形AEFM是平行四边形,可得出AM=EF,AE=MF,再通过证三角形全等,得出AE=CF,可得出BA2=BF2+2BF![]() AE+AE2(1),再在Rt△ABM中,利用勾股定理得出MA2=AB2+BF2-2BF
AE+AE2(1),再在Rt△ABM中,利用勾股定理得出MA2=AB2+BF2-2BF![]() AE+AE2(2),然后由(1)+(2),可求出结果.
AE+AE2(2),然后由(1)+(2),可求出结果.
过点A作AM∥EF交BC于点M
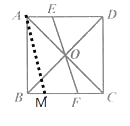
∵正方形ABCD
∴AD∥BC,OA=OC
∠EAO=∠FCO
在△AOE和△COF中
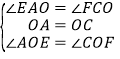
∴△AOE≌△COF(ASA)
∴AE=CF
∴BC=BF+FC
BA2=BC2=(BF+AE)2,
即BA2=BF2+2BF![]() AE+AE2(1)
AE+AE2(1)
∵AD∥BC,AM∥EF
∴四边形AEFM是平行四边形
∴AE=MF,AM=EF=6
∴BM=BF-MF=BF-AE
在Rt△ABM中
MA2=AB2+(BF-AE)2=AB2+BF2-2BF![]() AE+AE2(2)
AE+AE2(2)
由(1)+(2)得
BA2+EF2=BF2+2BF![]() AE+AE2+AB2+BF2-2BF
AE+AE2+AB2+BF2-2BF![]() AE+AE2
AE+AE2
36=2BF2+2AE2
∴AE2+BF2=18
故选:C.


科目:初中数学 来源: 题型:
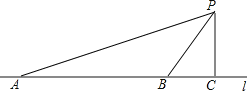
【题目】汽车超速行驶是交通安全的重大隐患,为了有效降低交通事故的发生,许多道路在事故易发路段设置了区间测速如图,学校附近有一条笔直的公路l,其间设有区间测速,所有车辆限速40千米/小时数学实践活动小组设计了如下活动:在l上确定A,B两点,并在AB路段进行区间测速.在l外取一点P,作PC⊥l,垂足为点C.测得PC=30米,∠APC=71°,∠BPC=35°.上午9时测得一汽车从点A到点B用时6秒,请你用所学的数学知识说明该车是否超速.(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随州市新水一桥(如图1)设计灵感来源于市花﹣﹣兰花,采用蝴蝶兰斜拉桥方案,设计长度为258米,宽32米,为双向六车道,2018年4月3日通车.斜拉桥又称斜张桥,主要由索塔、主梁、斜拉索组成.某座斜拉桥的部分截面图如图2所示,索塔AB和斜拉索(图中只画出最短的斜拉索DE和最长的斜拉索AC)均在同一水平面内,BC在水平桥面上.已知∠ABC=∠DEB=45°,∠ACB=30°,BE=6米,AB=5BD.
(1)求最短的斜拉索DE的长;
(2)求最长的斜拉索AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若DE=8,则线段BD+CE的长为
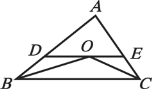
A. 5B. 6C. 7D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
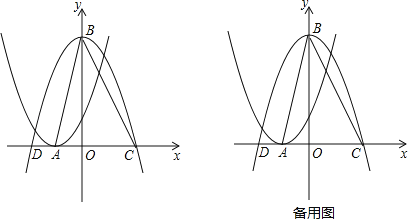
【题目】如图所示,将二次函数y=x2+2x+1的图象沿x轴翻折,然后向右平移1个单位,再向上平移4个单位,得到二次函数y=ax2+bx+c的图象.函数y=x2+2x+1的图象的顶点为点A.函数y=ax2+bx+c的图象的顶点为点B,和x轴的交点为点C,D(点D位于点C的左侧).
(1)求函数y=ax2+bx+c的解析式;
(2)从点A,C,D三个点中任取两个点和点B构造三角形,求构造的三角形是等腰三角形的概率;
(3)若点M是线段BC上的动点,点N是△ABC三边上的动点,是否存在以AM为斜边的Rt△AMN,使△AMN的面积为△ABC面积的![]() ?若存在,求tan∠MAN的值;若不存在,请说明理由.
?若存在,求tan∠MAN的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
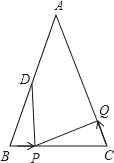
【题目】如图,已知△ABC中,AB=6cm,∠B=∠C,BC=4cm,点D为AB的中点.若点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入相应的大括号内.
3![]() ,-
,-![]() ,
,![]() ,0.5,2π,3.14159265,-
,0.5,2π,3.14159265,-![]() ,1.103030030003…(相
,1.103030030003…(相
邻两个3之间依次多1个0).
(1) 有理数集合:{ };
(2) 无理数集合:{ };
(3) 实数集合:{ };
(4) 负实数集合:{ }.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一扇窗户如图1所示,窗框和窗扇用“滑块铰链”连接.如图2是图1中“滑块铰链”的平面示意图,滑轨MN安装在窗框上,托悬臂DE安装在窗扇上,支点4处装有滑块,滑块可以左右滑动,支点B,C,D在一条直线上,延长DE交MN于点F.已知AC=DE=20cm,AE=CD=10cm,BD=40cm.

(1)当∠CAB=35 时,求窗扇与窗框的夹角∠DFB的度数.
(2)当窗扇关闭时,图中点E,A,D,C,B都在滑轨MN上.求此时点A与点B之间的距离.
(3)在(2)的前提下,将窗户推开至四边形ACDE为矩形时,求点A处的滑块移动的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是今年雨季某河流一周的水位变化情况(上周末的水位达到警戒水位)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位记录 |
|
|
|
|
|
|
|
注:此河流的警戒水位为![]() 米.
米.
![]() 完成下面的本周水位变化记录表:
完成下面的本周水位变化记录表:
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化 |
|
|
|
(注:规定水位比前一天上升用“![]() ”,水位比前一天下降用“
”,水位比前一天下降用“![]() ”,不升不降记作“
”,不升不降记作“![]() ”.)
”.)
![]() 与上周末相比,本周末河流水位是上升了还是下降了? (填“上升”或“下降”)
与上周末相比,本周末河流水位是上升了还是下降了? (填“上升”或“下降”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com