
”¾ĢāÄæ”æŌĶĮĻĀĮŠ²ÄĮĻ£ŗ
ĪŹĢā£ŗČēĶ¼ĖłŹ¾£¬ŌŚÕż·½ŠĪABCDŗĶBEFGÖŠ£¬µćA£¬B£¬EŌŚĶ¬Ņ»Ö±ĻßÉĻ£¬PŹĒĻ߶ĪDFÖŠµć£¬Į¬½ÓPG£¬PC£®
Ģ½¾æ£ŗµ±PGÓėPCµÄ¼Š½ĒĪŖ90”揱£¬Ę½ŠŠĖıߊĪBEFGŹĒÕż·½ŠĪ£®
Š”“ĻĶ¬Ń§µÄĖ¼Ā·ŹĒ£ŗŹ×ĻČæÉŅŌÖ¤Ć÷ĖıߊĪBEFGŹĒ¾ŲŠĪ£¬Č»ŗóŃÓ³¤GP½»DCÓŚµćH£¬¹¹ŌģČ«µČČż½ĒŠĪ£¬¾¹żĶĘĄķæÉŅŌĢ½Ė÷³öĪŹĢā“š°ø£®
ĒėÄć²Ī漊”“ĻĶ¬Ń§µÄĖ¼Ā·£¬Ģ½¾æ²¢½ā¾öÕāøöĪŹĢā£®
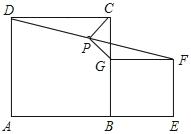
£Ø1£©ĒóÖ¤£ŗĖıߊĪBEFGŹĒ¾ŲŠĪ£»
£Ø2£©ĒóÖ¤£ŗPGÓėPCµÄ¼Š½ĒĪŖ90”揱£¬ĖıߊĪBEFGŹĒÕż·½ŠĪ£®
”¾“š°ø”æ¼ū½āĪö
”¾½āĪö”æÖ¤Ć÷£ŗ£Ø1£©ŌŚÕż·½ŠĪABCDÖŠ£¬”ĻABC=90”ć£¬
”ą”ĻEBG=90”ć£¬
”ßĖıߊĪBEFGŹĒĘ½ŠŠĖıߊĪ£¬
”ąĘ½ŠŠĖıߊĪBEFGŹĒ¾ŲŠĪ£¬
£Ø2£©ČēĶ¼£¬
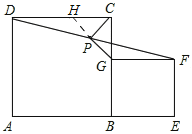
ŃÓ³¤GP½»DCÓŚµćH£¬
”ßŌŚÕż·½ŠĪABCDŗĶBEFGÖŠ£¬
”ąAB”ĪDC£¬RE”ĪGF£¬
”ąDC”ĪGF£¬
”ą”ĻHDP=”ĻGFP£¬”ĻDHP=”ĻFGP£¬
”ßµćPŹĒĻ߶ĪDFÖŠµć£¬
”ąDP=FP£¬
”ą”÷DHP”Õ”÷FGP£¬
”ąDH=FG£¬HP=GP£¬
”ß”ĻCPG=90”ć£¬
”ąCH=CG£¬
ŌŚÕż·½ŠĪABCDÖŠ£¬DC=BC£¬
”ąDH=BG£¬
”ąBG=GF£¬
ÓÉ£Ø1£©ÖŖ£¬ĖıߊĪBEFGŹĒ¾ŲŠĪ£¬
”ąĖıߊĪBEFGŹĒÕż·½ŠĪ£®


 »ĘøŌĢģĢģĮ·æŚĖćĢāæØĻµĮŠ“š°ø
»ĘøŌĢģĢģĮ·æŚĖćĢāæØĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖĮĖ½āijŹŠ¾ÅÄź¼¶Ń§ÉśŃ§Ņµæ¼ŹŌĢåÓż³É¼Ø£¬ĻÖĖ껜³éČ”²æ·ÖѧɜµÄĢåÓż£ØA£ŗ50·Ö£»B£ŗ49©45·Ö£»C£ŗ44©40·Ö£»D£ŗ39©30·Ö£»E£ŗ29©0·Ö£©³É¼Ø½ųŠŠ·Ö¶ĪĶ³¼ĘČēĻĀ£ŗ

øł¾ŻÉĻĆęĢį¹©µÄŠÅĻ¢£¬»Ų“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©ŌŚĶ³¼Ę±ķÖŠ£¬aµÄÖµĪŖ £¬bµÄÖµĪŖ £»
£Ø2£©½«Ķ³¼ĘĶ¼²¹³äĶźÕū£»
£Ø3£©Čē¹ū°Ń³É¼ØŌŚ40·ÖŅŌÉĻ£Øŗ¬40·Ö£©¶ØĪŖÓÅŠć£¬ÄĒĆ“øĆŹŠ½ńÄź10560Ćū¾ÅÄź¼¶Ń§ÉśÖŠĢåÓż³É¼ØĪŖÓÅŠćµÄѧɜČĖŹżŌ¼ÓŠ¶ąÉŁĆū£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖÖ±Ļßy=©![]() x+2·Ö±š½»x”¢yÖįÓŚµćA”¢B£¬µćCĪŖĻ߶ĪOAµÄÖŠµć£¬¶ÆµćP“Ó×ų±źŌµć³ö·¢£¬ŅŌ2øöµ„Ī»³¤¶Č/ĆėµÄĖŁ¶ČĻņÖÕµćAŌĖ¶Æ£¬¶ÆµćQ“ÓµćC³ö·¢£¬ŅŌ
x+2·Ö±š½»x”¢yÖįÓŚµćA”¢B£¬µćCĪŖĻ߶ĪOAµÄÖŠµć£¬¶ÆµćP“Ó×ų±źŌµć³ö·¢£¬ŅŌ2øöµ„Ī»³¤¶Č/ĆėµÄĖŁ¶ČĻņÖÕµćAŌĖ¶Æ£¬¶ÆµćQ“ÓµćC³ö·¢£¬ŅŌ![]() øöµ„Ī»³¤¶Č/ĆėµÄĖŁ¶ČĻņÖÕµćBŌĖ¶Æ£®¹żµćQ×÷QM”ĪAB½»xÖįÓŚµćM£¬¶ÆµćP”¢QĶ¬Ź±³ö·¢£¬ĘäÖŠŅ»øöµćµ½“ļÖÕµć£¬ĮķŅ»øöµćŅ²Ķ£Ö¹ŌĖ¶Æ£¬ÉčµćPŌĖ¶ÆµÄŹ±¼äĪŖtĆė£¬PMµÄ³¤ĪŖyøöµ„Ī»³¤¶Č£®
øöµ„Ī»³¤¶Č/ĆėµÄĖŁ¶ČĻņÖÕµćBŌĖ¶Æ£®¹żµćQ×÷QM”ĪAB½»xÖįÓŚµćM£¬¶ÆµćP”¢QĶ¬Ź±³ö·¢£¬ĘäÖŠŅ»øöµćµ½“ļÖÕµć£¬ĮķŅ»øöµćŅ²Ķ£Ö¹ŌĖ¶Æ£¬ÉčµćPŌĖ¶ÆµÄŹ±¼äĪŖtĆė£¬PMµÄ³¤ĪŖyøöµ„Ī»³¤¶Č£®
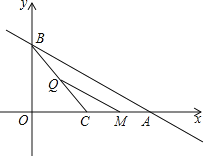
£Ø1£©”ĻBCO= ”ć£»
£Ø2£©Ēóy¹ŲÓŚtµÄŗÆŹż¹ŲĻµŹ½¼°×Ō±äĮætµÄȔֵ·¶Ī§£»
£Ø3£©ŹĒ·ń“ęŌŚŹ±¼ät£¬Ź¹µĆŅŌPCĪŖÖ±¾¶µÄ”ŃDÓėÖ±ĻßQMĻąĒŠ£æČō“ęŌŚ£¬ĒótµÄÖµ£»²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼×”¢ŅŅĮ½ÖÖĖ®µ¾ŹŌŃéĢļĮ¬Šų5ÄźµÄĘ½¾łµ„Ī»Ć껿²śĮæČēĻĀ£ŗ£Øµ„Ī»£ŗ¶Ö/¹«Ēź£©
Ę·ÖÖ | µŚ1Äź | µŚ2Äź | µŚ3Äź | µŚ4Äź | µŚ5 Äź |
¼× | 9.8 | 9.9 | 10.1 | 10 | 10.2 |
ŅŅ | 9.4 | 10.3 | 10.8 | 9.7 | 9.8 |
£Ø1£©ÄÄÖÖĖ®µ¾µÄĘ½¾łµ„Ī»Ć껿²śĮæ±Č½Ļøߣæ
£Ø2£©ÄÄÖÖĖ®µ¾µÄ²śĮæ±Č½ĻĪČ¶Ø£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ŹĒij¹«Ō°ĄļŅ»“¦¾ŲŠĪ·ē¾°ŠĄÉĶĒųABCD£¬³¤AB£½50Ć×£¬æķBC£½25Ć×£¬ĪŖ·½±ćÓĪČĖ¹ŪÉĶ£¬¹«Ō°ĢŲŅāŠŽ½ØĮĖČēĶ¼ĖłŹ¾µÄŠ”Ā·(Ķ¼ÖŠ·ĒŅõÓ°²æ·Ö)£¬Š”Ā·µÄæķ¾łĪŖ1Ć×£¬ÄĒŠ”Ć÷ŃŲ×ÅŠ”Ā·µÄÖŠ¼ä£¬“Ó³öæŚAµ½³öæŚBĖł×ßµÄĀ·Ļß(Ķ¼ÖŠŠéĻß)³¤ĪŖ___________

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ”õABCDÖŠ£¬Ö±ĻßmČʵćAŠż×Ŗ£¬Ö±Ļßm²»¾¹żB”¢C”¢Dµć£¬¹żB”¢C”¢D·Ö±š×÷BE”ĶmÓŚE£¬ CF”ĶmÓŚF£¬ DG”ĶmÓŚG£®
£Ø1£©µ±Ö±ĻßmŠż×Ŗµ½ČēĶ¼1Ī»ÖĆŹ±£¬Ļ߶ĪBE”¢CF”¢DGÖ®¼äµÄŹżĮæ¹ŲĻµŹĒ _£»
£Ø2£©µ±Ö±ĻßmŠż×Ŗµ½ČēĶ¼2Ī»ÖĆŹ±£¬Ļ߶ĪBE”¢CF”¢DGÖ®¼äµÄŹżĮæ¹ŲĻµŹĒ _£»
£Ø3£©µ±Ö±ĻßmŠż×Ŗµ½ČēĶ¼3µÄĪ»ÖĆŹ±£¬Ļ߶ĪBE”¢CF”¢DGÖ®¼äÓŠŌõŃłµÄŹżĮæ¹ŲĻµ£æĒėÖ±½ÓŠ“³öÄćµÄ²ĀĻė£¬²¢¼ÓŅŌÖ¤Ć÷£®
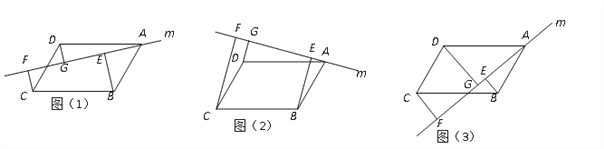
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µćEŌŚÖ±ĻßDFÉĻ£¬µćBŌŚÖ±ĻßACÉĻ£¬Čō”Ļ1£½”Ļ2£¬”Ļ3£½”Ļ4£¬Ōņ”ĻA£½”ĻF£¬ĒėĖµĆ÷ĄķÓÉ£®

½ā£ŗ”ß”Ļ1£½”Ļ2£ØŅŃÖŖ£©
”Ļ2£½”ĻDGF£Ø £©
”ą”Ļ1£½”ĻDGF
”ąBD”ĪCE£Ø £©
”ą”Ļ3£«”ĻC£½180£Ø £©
Ó֔ߔĻ3£½”Ļ4£ØŅŃÖŖ£©
”ą”Ļ4£«”ĻC£½180
”ą ”Ī £ØĶ¬ÅŌÄŚ½Ē»„²¹£¬Į½Ö±ĻßĘ½ŠŠ£©
”ą”ĻA£½”ĻF£Ø £©
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com