
【题目】已知抛物线y=x2﹣(2m+1)x+2m不经过第三象限,且当x>2时,函数值y随x的增大而增大,则实数m的取值范围是( )
A.0≤m≤1.5
B.m≥1.5
C.0≤m≤1
D.0<m≤1.5
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴正半轴交于点A(3,0),与y轴交于点B(0,3),点P是x轴上一动点,过点P作x轴的垂线交抛物线于点C,交直线AB于点D,设P(x,0).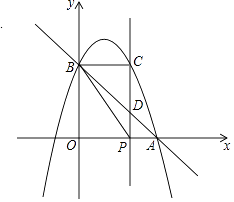
(1)求抛物线的函数表达式;
(2)当0<x<3时,求线段CD的最大值;
(3)在△PDB和△CDB中,当其中一个三角形的面积是另一个三角形面积的2倍时,求相应x的值;
(4)过点B,C,P的外接圆恰好经过点A时,x的值为 . (直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() 是过
是过![]() 点的一条直线
点的一条直线![]()
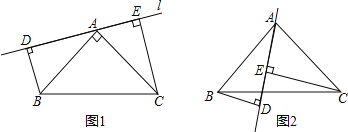
(1)作![]() 于点
于点![]() ,
,![]()
![]() 点,若
点,若![]() 点和
点和![]() 点在直线
点在直线![]() 的同侧,求证:
的同侧,求证:![]() ;
;
(2)若直线![]() 绕点
绕点![]() 旋转到
旋转到![]() 点和
点和![]() 点在其两侧,其余条件不变,问:
点在其两侧,其余条件不变,问:![]() 的关系如何?请予以证明.
的关系如何?请予以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
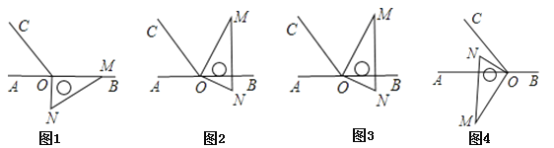
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°.将一直角三角板MON的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)求∠CON的度数;
(2)如图2是将图1中的三角板绕点O按每秒15°的速度沿逆时针方向旋转一周的情况,在旋转的过程中,第t秒时,三条射线OA、OC、OM构成两个相等的角,求此时的t值
(3)将图1中的三角板绕点O顺时针旋转至图3(使ON在∠AOC的外部),图4(使ON在∠AOC的内部)请分别探究∠AOM与∠NOC之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下,![]() 不成立,但有些数可以使得它成立,例如:a=1,b=2.我们称使得
不成立,但有些数可以使得它成立,例如:a=1,b=2.我们称使得![]() 成立的一对数a,b为“相伴数对”,记为(a,b).
成立的一对数a,b为“相伴数对”,记为(a,b).
(1)判断数对(﹣2,1),(3,3)是否是“相伴数对”;
(2)若(k,﹣1)是“相伴数对”,求k的值;
(3)若(4,m)是“相伴数对”,求代数式![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC的一角折叠,使点C落在△ABC内一点
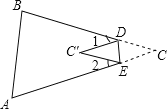
(1)若∠1=40°,∠2=30°,求∠C的度数;(2)试通过第(1)问,直接写出∠1、∠2、∠C三者之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=![]() BC,连接CD和EF.
BC,连接CD和EF.
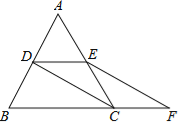
(1)求证:DE=CF;
(2)求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com