
分析 (1)先把各二次根式化为最简二次根式,然后去括号后合并即可.
(2)先根据积的乘方得到原式=[($\sqrt{3}$-$\sqrt{2}$)($\sqrt{3}$+$\sqrt{2}$)]3($\sqrt{3}$+$\sqrt{2}$)2,然后利用平方差公式和乘法根式计算.
解答 解:(1)$\sqrt{8}$-$\frac{1}{8}$$\sqrt{48}$-($\frac{2}{3}$$\sqrt{4\frac{1}{2}}$-2$\sqrt{\frac{3}{4}}$)
=2$\sqrt{2}$-$\frac{1}{2}$$\sqrt{3}$-($\sqrt{2}$-$\sqrt{3}$)
=2$\sqrt{2}$-$\frac{1}{2}$$\sqrt{3}$-$\sqrt{2}$+$\sqrt{3}$
=$\sqrt{2}$+$\frac{1}{2}$$\sqrt{3}$;
(2)($\sqrt{3}$-$\sqrt{2}$)3•($\sqrt{3}$+$\sqrt{2}$)5
=[($\sqrt{3}$-$\sqrt{2}$)($\sqrt{3}$+$\sqrt{2}$)]3($\sqrt{3}$+$\sqrt{2}$)2
=13×($\sqrt{3}$+$\sqrt{2}$)2
=5+2$\sqrt{6}$.
点评 本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.


科目:初中数学 来源: 题型:填空题
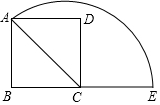 如图,在正方形ABCD中,AB=2,连接AC,以点C为圆心、AC长为半径画弧,与BC的延长线交于点E,则图中$\widehat{AE}$的长为$\frac{3\sqrt{2}}{2}$π.
如图,在正方形ABCD中,AB=2,连接AC,以点C为圆心、AC长为半径画弧,与BC的延长线交于点E,则图中$\widehat{AE}$的长为$\frac{3\sqrt{2}}{2}$π.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
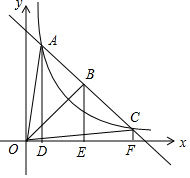 如图,直线l与函数y=$\frac{k}{x}$的图象相交,A、B、C是直线l的三点,过点A、B、C分别作x轴的垂线,垂足分别为D、E、F,连接OA、OB、OC,设△OAD的面积是S1,△OBE的面积是S2,△OCF的面积是S3,则( )
如图,直线l与函数y=$\frac{k}{x}$的图象相交,A、B、C是直线l的三点,过点A、B、C分别作x轴的垂线,垂足分别为D、E、F,连接OA、OB、OC,设△OAD的面积是S1,△OBE的面积是S2,△OCF的面积是S3,则( )| A. | S1<S2<S3 | B. | S1=S2=S3 | C. | S2>S1>S3 | D. | S3=S1<S2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
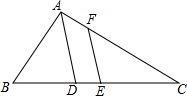 如图,△ABC中,E是BC中点,AD是∠BAC的平分线,EF∥AD交AC于F.若AB=11,AC=15,则FC的长为( )
如图,△ABC中,E是BC中点,AD是∠BAC的平分线,EF∥AD交AC于F.若AB=11,AC=15,则FC的长为( )| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
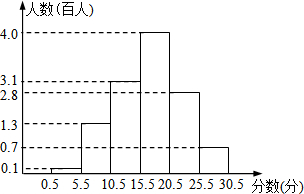 2017年3月27日是第22个全国中小学生安全教育日,某校为增强学生的安全意识,组织全校学生参加安全知识测试,并对测试成绩做了详细统计,将测试成绩(成绩都是整数,试卷满分30分)绘制成了如下“频数分布直方图”,请回答:
2017年3月27日是第22个全国中小学生安全教育日,某校为增强学生的安全意识,组织全校学生参加安全知识测试,并对测试成绩做了详细统计,将测试成绩(成绩都是整数,试卷满分30分)绘制成了如下“频数分布直方图”,请回答:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
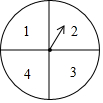 由于只有1张市运动会开幕式的门票,小王和小张都想去,两人商量采取转转盘(如图,转盘盘面被分为面积相等,且标有数字1,2,3,4的4个扇形区域)的游戏方式决定谁胜谁去观看.规则如下:两人各转动转盘一次,当转盘指针停止,如两次指针对应盘面数字都是奇数,则小王胜;如两次指针对应盘面数字都是偶数,则小张胜;如两次指针对应盘面数字是一奇一偶,视为平局.若为平局,继续上述游戏,直至分出胜负.
由于只有1张市运动会开幕式的门票,小王和小张都想去,两人商量采取转转盘(如图,转盘盘面被分为面积相等,且标有数字1,2,3,4的4个扇形区域)的游戏方式决定谁胜谁去观看.规则如下:两人各转动转盘一次,当转盘指针停止,如两次指针对应盘面数字都是奇数,则小王胜;如两次指针对应盘面数字都是偶数,则小张胜;如两次指针对应盘面数字是一奇一偶,视为平局.若为平局,继续上述游戏,直至分出胜负.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com