
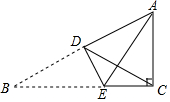
 如图,△ABC中,∠C=90°,∠B=30°,将△ABC折叠,使点B落在点A处,DE为折痕,在下列结论中:
如图,△ABC中,∠C=90°,∠B=30°,将△ABC折叠,使点B落在点A处,DE为折痕,在下列结论中:| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
分析 ①根据折叠的性质即可得出结论;
②根据△ADE≌△BDE可知∠ADE=∠BDE=90°,AE=BE,进而可得出结论;
③由∠B=30°可知∠BAC=60°,AC=$\frac{1}{2}$AB,故可得出结论;
④由△ADE≌△BDE,∠B=30°可得出∠DAE=30°,再由△ACD是等边三角形即可得出结论;
⑤由∠DAE=30°可知AE是∠BAC的平分线,故DE=CE,再由∠B=30°可得出DE=$\frac{1}{2}$BE,故可得出结论;
⑥根据锐角三角函数的定义可得出结论.
解答 解:①∵△ADE由△BDE翻折而成,
∴△ADE≌△BDE,故本小题正确;
②∵△ADE≌△BDE,
∴∠ADE=∠BDE=90°,AE=BE,
∴DE垂直平分AB,故本小题正确;
③∵∠B=30°,
∴∠BAC=60°,AC=$\frac{1}{2}$AB,
∴AC=AD,
∴△ADC是等边三角形,故本小题正确;
④∵△ADE≌△BDE,∠B=30°,
∴∠DAE=30°,
∴AD是∠BAC的平分线.
∵△ACD是等边三角形,
∴AE垂直平分CD,故本小题正确;
⑤∵AE是∠BAC的平分线,DE⊥AB,AC⊥BC,
∴DE=CE.
∵∠B=30°,
∴DE=$\frac{1}{2}$BE,
∴BE=2EC,故本小题正确;
⑥∵∠CAE=30°,
∴AC=$\frac{CE}{tan30°}$.
∵∠B=30°,
∴AB=2AC,
∴AB=2×$\frac{CE}{\frac{\sqrt{3}}{3}}$=2$\sqrt{3}$CE,故本小题错误.
故选C.
点评 本题考查的是翻折变换,熟知图形翻折不变性的性质是解答此题的关键.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:解答题
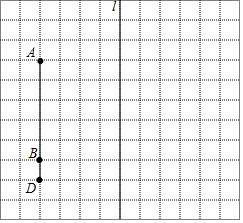 如图,在正方形网格中,每个小正方形的边长为1个单位长度.线段AD的两个端点都在格点上,点B是线段AD上的格点,且BD=1,直线l在格线上.
如图,在正方形网格中,每个小正方形的边长为1个单位长度.线段AD的两个端点都在格点上,点B是线段AD上的格点,且BD=1,直线l在格线上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 838 | B. | 924 | C. | 924或838 | D. | 838或910 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x-2)(x+1) | B. | y=$\frac{1}{2}$(x+1)2 | C. | y=2(x+3)2-2x2 | D. | y=1-$\sqrt{3}$x2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com