
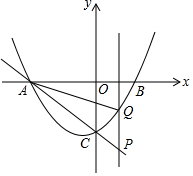
 ��֪������y=$\frac{1}{4}$x2+$\frac{1}{4}$x-3��x����A��B���㣬��y���ڵ�C����P��ֱ��AC�ϵ�һ�����㣬����P��PQ��x�ᣬ���������ڵ�Q������CQ�����P�ĺ�����Ϊm��
��֪������y=$\frac{1}{4}$x2+$\frac{1}{4}$x-3��x����A��B���㣬��y���ڵ�C����P��ֱ��AC�ϵ�һ�����㣬����P��PQ��x�ᣬ���������ڵ�Q������CQ�����P�ĺ�����Ϊm������ ��1���������߽���ʽ�����A��C���꣬���ô���ϵ���������ֱ��AC����ʽ��
��2������m�ֱ��ʾ��P��Q�����꣬�����m��ʾ��PQ��PC�ij����������ɵõ�����m�ķ��̣������m��ֵ��
��3����ACΪֱ����Բ������AQCΪ�۽�ʱ�����QӦ��Բ�ڣ����ͼ�����õ�Q��λ�ã������m��ȡֵ��Χ��
��� �⣺
��1����y=$\frac{1}{4}$x2+$\frac{1}{4}$x-3��
��y=0�ɵã�0=$\frac{1}{4}$x2+$\frac{1}{4}$x-3�����x=-4��x=3��
��A��-4��0����B��3��0����
��x=0�ɵ�y=-3��
��C��0��-3����
��ֱ��AC����ʽΪy=kx+b��
��A��C�������ɵ�$\left\{\begin{array}{l}{-4k+b=0}\\{b=-3}\end{array}\right.$�����$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=-3}\end{array}\right.$��
��ֱ��AC����ʽΪy=-$\frac{3}{4}$x-3��
��2����P����ֱ��AC�ϣ���Q���������ϣ���P�������Ϊm��
��P��m��-$\frac{3}{4}$m-3����Q��m��$\frac{1}{4}$m2+$\frac{1}{4}$m-3����
��PQ=|$\frac{1}{4}$m2+$\frac{1}{4}$m-3-��-$\frac{3}{4}$m-3��|=|$\frac{1}{4}$m2+m|��
��C��0��-3����
��PC=$\sqrt{{m}^{2}+[-\frac{3}{4}m-3-��-3��]^{2}}$=$\frac{5}{4}$|m|��
����PCQ�ǡ�CPQΪ���ǵĵ���������ʱ������PC=PQ��
��|$\frac{1}{4}$m2+m|=$\frac{5}{4}$|m|����$\frac{1}{4}$m2+m=��$\frac{5}{4}$m��
��$\frac{1}{4}$m2+m=$\frac{5}{4}$mʱ�����m=0��m=1��
��m=0����P��C�غϣ���ȥ��
��m=1��
��$\frac{1}{4}$m2+m=-$\frac{5}{4}$mʱ�����m=-6��m=0����ȥ����
��m=-6��
���Ͽ�֪�������������ĵ�P����ʱm��ֵΪ1��-6��
��3����ACΪֱ����Բ����ͼ��
����AQCΪ�۽�ʱ�����֪��Q��Բ�ڣ�
���Q���߶�AC�·����������ϣ�
��-4��m��0��
�ʴ�Ϊ��-4��m��0��
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰����ϵ���������������ε����ʡ����ɶ�����Բ�ܽǶ��������ν��˼���֪ʶ�㣮�ڣ�1�������A��C�������ǽ���Ĺؼ����ڣ�2������m��ʾ��PQ��PC�ij����ǽ���Ĺؼ����ڣ�3����ȷ����Q�����ڵ�λ���ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��������IJ�ֵ ����λ��ǧ�ˣ� | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
| ���� | 1 | 4 | 2 | -1 | 4 | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 27 | B�� | -3 | C�� | 9 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 С���Ͱְֽ��е�ɽ����������ͬʱ��ɽ���³���������ͬ·��������ɽ��С����8���ӵ���ɽ������ʱ�ְ־������280�ף�С������ɽ��������ԭ·������ɽ����ְ������Ͱְ�һ����ԭ��ɽ�ٶȷ��س����أ�С�����ְ��ڶ���������������ص�·��y1���ף���y2���ף���С��������ʱ��x���֣��ĺ�����ϵ��ͼ��
С���Ͱְֽ��е�ɽ����������ͬʱ��ɽ���³���������ͬ·��������ɽ��С����8���ӵ���ɽ������ʱ�ְ־������280�ף�С������ɽ��������ԭ·������ɽ����ְ������Ͱְ�һ����ԭ��ɽ�ٶȷ��س����أ�С�����ְ��ڶ���������������ص�·��y1���ף���y2���ף���С��������ʱ��x���֣��ĺ�����ϵ��ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
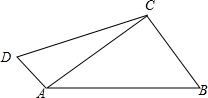 ��֪����ͼ���ı���ABCD�У���ACB=90�㣬AB=15��BC=9��AD=5��DC=13����֤����ACD��ֱ�������Σ�
��֪����ͼ���ı���ABCD�У���ACB=90�㣬AB=15��BC=9��AD=5��DC=13����֤����ACD��ֱ�������Σ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com