
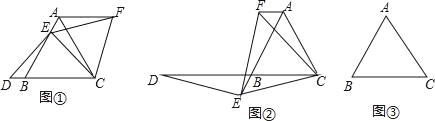
【题目】【问题提出】
如图①,已知△ABC是等腰三角形,点E在线段AB上,点D在直线BC上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF连接EF
试证明:AB=DB+AF
【类比探究】
(1)如图②,如果点E在线段AB的延长线上,其他条件不变,线段AB,DB,AF之间又有怎样的数量关系?请说明理由
(2)如果点E在线段BA的延长线上,其他条件不变,请在图③的基础上将图形补充完整,并写出AB,DB,AF之间的数量关系,不必说明理由.
【答案】证明见解析;(1)AB=BD﹣AF;(2)AF=AB+BD.
【解析】试题分析:(1)根据旋转的性质得出△EDB与FEA全等的条件BE=AF,再结合已知条件和旋转的性质推出∠D=∠AEF,∠EBD=∠EAF=120°,得出△EDB≌FEA,所以BD=AF,等量代换即可得出结论.(2)先画出图形证明∴△DEB≌△EFA,方法类似于(1);(3)画出图形根据图形直接写出结论即可.
试题解析:(1)证明:DE=CE=CF,△BCE
由旋转60°得△ACF,
∴∠ECF=60°,BE=AF,CE=CF,
∴△CEF是等边三角形,
∴EF=CE,
∴DE=EF,∠CAF=∠BAC=60°,
∴∠EAF=∠BAC+∠CAF=120°,
∵∠DBE=120°,
∴∠EAF=∠DBE,
又∵A,E,C,F四点共圆,
∴∠AEF=∠ACF,
又∵ED=DC,
∴∠D=∠BCE,∠BCE=∠ACF,
∴∠D=∠AEF,
∴△EDB≌FEA,
∴BD=AF,AB=AE+BF,
∴AB=BD+AF.
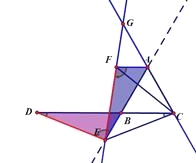
类比探究(1)DE=CE=CF,△BCE由旋转60°得△ACF,
∴∠ECF=60°,BE=AF,CE=CF,
∴△CEF是等边三角形,
∴EF=CE,
∴DE=EF,∠EFC=∠BAC=60°,
∠EFC=∠FGC+∠FCG,∠BAC=∠FGC+∠FEA,
∴∠FCG=∠FEA,
又∠FCG=∠EAD
∠D=∠EAD,
∴∠D=∠FEA,
由旋转知∠CBE=∠CAF=120°,
∴∠DBE=∠FAE=60°
∴△DEB≌△EFA,
∴BD=AE, EB=AF,
∴BD=FA+AB.
即AB=BD-AF.
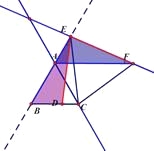
(2)AF=BD+AB(或AB=AF-BD)


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料、并完成任务.
无限循环小数化分数
我们知道分数![]() 写出小数形式即
写出小数形式即![]() ,反过来,无限循环小数
,反过来,无限循环小数![]() 写成分数形式即
写成分数形式即![]() ,一般地,任何一个无限循环小数都可以写成分数形式.
,一般地,任何一个无限循环小数都可以写成分数形式.
先以无限循环小数![]() 为例进行讨论.
为例进行讨论.
设![]() ,由
,由![]() 可知,
可知,![]() ,所以
,所以![]() ,解方程,得
,解方程,得![]() ,于是,得
,于是,得![]() .
.
再以无限循环小数![]() 为例,做进一步的讨论.
为例,做进一步的讨论.
无限循环小数![]() ,它的循环节有两位,类比上面的讨论可以想到如下做法.
,它的循环节有两位,类比上面的讨论可以想到如下做法.
设![]() ,由
,由![]() 可知,
可知,![]() .
.
所以![]() .解方程,得
.解方程,得![]() ,于是,
,于是,![]() .
.
类比应用(直接写出答案,不写过程)
①![]() .②
.②![]() .③
.③![]() .
.
能力提升
将![]() 化为分数形式,写出过程.
化为分数形式,写出过程.
拓展探究
①![]() ;
;
②比较大小![]() 1(填“
1(填“![]() ”或“
”或“![]() ”或“
”或“![]() ”);
”);
③若![]() ,则
,则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的A′处,若AO=OB=2,则阴影部分面积为( )
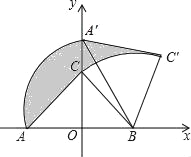
A. ![]() π B.
π B. ![]() π﹣1 C.
π﹣1 C. ![]() +1 D.
+1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:
,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
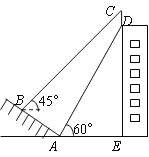
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用了随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.

请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 .
(2)请补全条形统计图.
(3)若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用画树状图或列表的方法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将图①中的正方形剪开得到图②,图②中共有4个正方形;将图②中一个正方形剪开得到图③,图③中共有7个正方形;将图③中一个正方形剪开得到图④,图④中共有10个正方形……如此下去,则第2019个图中共有正方形的个数为( )
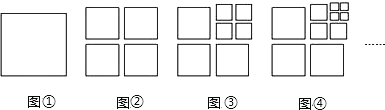
A.2019B.2021C.6049D.6055
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径OD⊥AB,与AC交于点E,与过点C的⊙O切线交于点D.
(1)若AC=6,BC=3,求OE的长.
(2)试判断∠A与∠CDE的数量关系,并说明理由.
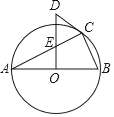
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校九年级举行乒乓球比赛,准备发放一些奖品进行奖励,奖品设为一等奖和二等奖.已知购买一个一等奖奖品比购买一个二等奖奖品多用20元.若用400元购买一等奖奖品的个数是用160元购买二等奖奖品个数的一半.
(1)求购买一个一等奖奖品和一个二等奖奖品各需多少元?
(2)经商谈,商店决定给予该学校购买一个一等奖奖品即赠送一个二等奖奖品的优惠,如果该学校需要二等奖奖品的个数是一等奖奖品个数的2倍还多8个,且该学校购买两个奖项奖品的总费用不超过670元,那么该学校最多可购买多少个一等奖奖品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM周长最小时,求点M的坐标及△ACM的最小周长.
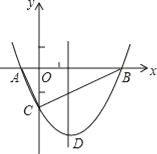
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com