
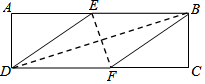
 �ھ���ABCD�У���һ������BFDE����E��F�ֱ����߶�AB��CD�ϣ��������ǵ�����ֱ�ΪSABCD��SBFDE���ָ����������⣺����$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$����tan��EDF=$\frac{\sqrt{3}}{3}$������DE2=BD•EF����DF=2AD��������
�ھ���ABCD�У���һ������BFDE����E��F�ֱ����߶�AB��CD�ϣ��������ǵ�����ֱ�ΪSABCD��SBFDE���ָ����������⣺����$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$����tan��EDF=$\frac{\sqrt{3}}{3}$������DE2=BD•EF����DF=2AD��������| A�� | ���Ǽ����⣬���Ǽ����� | B�� | ���������⣬���Ǽ����� | ||
| C�� | ���Ǽ����⣬���������� | D�� | ���������⣬���������� |
���� ������֪�����cos��BFC=$\frac{\sqrt{3}}{2}$�������tan��EDF�������жϣ�
����S��DEF=$\frac{1}{2}$DF•AD=$\frac{1}{4}$BD•EF����DE2=BD•EF���ɵ�DF•AD=$\frac{1}{2}$DF2����DF=2AD��
��� �⣺����CF=x��DF=y��BC=h��
���ı���BFDE�����Σ�
��BF=DF=y��DE��BF��
����$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$��
��$\frac{��x+y��h}{yh}$=$\frac{2+\sqrt{3}}{2}$��
��$\frac{x}{y}$=$\frac{\sqrt{3}}{2}$����cos��BFC=$\frac{\sqrt{3}}{2}$��
���BFC=30�㣬
��DE��BF��
���EDF=��BFC=30�㣬
��tan��EDF=$\frac{\sqrt{3}}{3}$��
���Ԣ��������⣮
�ڡ��ı���BFDE�����Σ�
��DF=DE��
��S��DEF=$\frac{1}{2}$DF•AD=$\frac{1}{4}$BD•EF��
�֡�DE2=BD•EF����֪����
��S��DEF=$\frac{1}{4}$DE2=$\frac{1}{4}$DF2��
��DF•AD=$\frac{1}{2}$DF2��
��DF=2AD��
���Ԣ��������⣮
��ѡD��
���� ���⿼���˾��ε����ʡ����ε����ʡ�������Ǻ����������ε������ʽ��֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�����������ȷ�������߶�֮��Ĺ�ϵ�������п��������ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 -3x+2=x2-5x+1��
-3x+2=x2-5x+1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
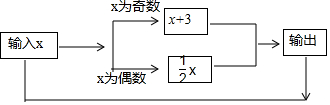
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��-1 | B�� | a��0 | C�� | a��1��a��0 | D�� | a��-1��a��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
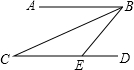 ��ͼ��AB��CD����E��CD�ϣ�BCƽ�֡�ABE������C=25�㣬���BED�Ķ����ǣ�������
��ͼ��AB��CD����E��CD�ϣ�BCƽ�֡�ABE������C=25�㣬���BED�Ķ����ǣ�������| A�� | 25�� | B�� | 45�� | C�� | 50�� | D�� | 75�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
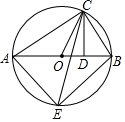 ��ͼ��Rt��ABC�ڽ��ڡ�O����ACB=90�㣬CD��AB�ڵ�D��CEƽ�֡�OCD��
��ͼ��Rt��ABC�ڽ��ڡ�O����ACB=90�㣬CD��AB�ڵ�D��CEƽ�֡�OCD���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com