【答案】
分析:(1)根据抛物线y=ax
2-2ax+b,可知对称轴方程,从而得到点A的坐标;再根据BC=10,梯形OABC的面积为18,可求B,C的坐标,再将O、B两点的坐标代入y=ax
2-2ax+b,运用待定系数法即可求出抛物线的解析式;
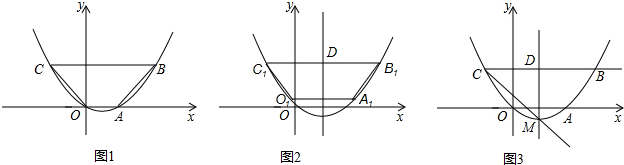
(2)在两条直线平移的过程中,梯形的上下底发生了改变,但是梯形的高没有变化,仍为3,即y
2-y
1=3,根据抛物线的解析式,用x
1、x
2表示出y
1、y
2,然后联立y
2-y
1=3,可得到第一个关于x
1、x
2的关系式①;在两条直线平移过程中,抛物线的对称轴没有变化,用x
1、x
2以及抛物线的对称轴的解析式表示出梯形上下底的长,进而得到梯形面积的表达式,这样得到另外一个x
1、x
2的关系式②,联立这两个关系式,得到关于(x
2-x
1)与S的关系式③,将S=36代入②③的关系式中,即可列方程组求得x
1、x
2的值,进而可求出点A
1的坐标;
(3)要解答此题,首先要弄清几个关键点:
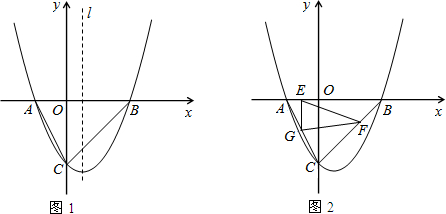
一、当PQ∥AB时,设直线AB与抛物线对称轴的交点为E,可得△DPQ∽△DBE,可用t表示出DP、DQ的长,而E点坐标易求得,根据相似三角形所得比例线段,即可得到此时t的值即t=

;
二、当P、Q都停止运动时,显然BC>DM,所以此时t=DM÷1=3

.
设直线PQ与直线AB的交点为F,与x轴的交点为G;假设直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似.显然t=

不合题意,舍去,所以分两种情况讨论:①当0<t<
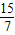
时,由题意知△FQE∽△FAG,得∠FGA=∠FEQ,由于BC∥x轴,则∠DPQ=∠FGA=∠FEQ,由此可证得△DPQ∽△DEB,DB、DE的长已求得,可用t表示出DP、DQ的长,根据相似三角形所得比例线段,即可求得此时t的值;
②当

<t<3

时,方法同①;
在求得t的值后,还要根据各自的取值范围将不合题意的解舍去.
解答:解:(1)∵y=ax
2-2ax+b=a(x-1)
2-a+b,
∴对称轴为:直线x=1,
∴点A的坐标为(2,0);
∵BC=10,梯形OABC的面积为18,
∴梯形OABC的高为:18×2÷(10+2)=3,
∴B(10÷2+1,3),即B(6,3),
C(1-10÷2,3),即C(-4,3).
将O(0,0),B(6,3)代入y=ax
2-2ax+b,
得

,
解得

,
∴抛物线解析式为:y=

x
2-

x;

(2)由题意得y
2-y
1=3,y
2-y
1=

x
22-

x
2-

x
12+

x
1=3,
得:(x
2-x
1)[

(x
2+x
1)-

]=3①,
S=

=3(x
1+x
2)-6,
得:x
1+x
2=

+2②,
把②代入①并整理得:x
2-x
1=
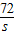
(S>0),
当s=36时,
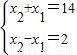
,
解得:
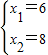
,
把x
1=6代入抛物线解析式,得y
1=

×6
2-

×6=3,
∴点A
1(6,3);
(3)存在t=

秒,可使直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似.理由如下:
易知直线AB的解析式为y=

x-

,可得直线AB与对称轴的交点E的坐标为(1,-

),
∴BD=5,DE=

,DP=5-t,DQ=t,
当PQ∥AB时,

=

,
即

=

,解得t=

.
设直线PQ与直线AB、x轴的交点分别为点F、G.假设直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似.下面分两种情况讨论:
①当0<t<

时,如图3-1;
∵△FQE∽△FAG,
∴∠FGA=∠FEQ,
∴∠DPQ=∠DEB;
易得△DPQ∽△DEB,
∴

,即

=

,
解得t=

>

,
∴t=

不合题意,舍去;

②当
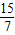
<t<3

时,如图3-2;
∵△FAG∽△FQE,
∴∠FAG=∠FQE,
∵∠DQP=∠FQE,∠FAG=∠EBD,
∴∠DQP=∠DBE,
易得△DPQ∽△DEB,
∴

,即

=

,
解得t=

,符合题意.
综上,可知当t=

秒时,直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似.
点评:本题考查了二次函数的综合类试题,涉及到:二次函数解析式的确定、等腰梯形的性质、图形面积的求法、相似三角形的判定和性质等重要知识;在(3)题中能够正确地画出图形,并准确地找到所求的三角形是解答此题的关键.

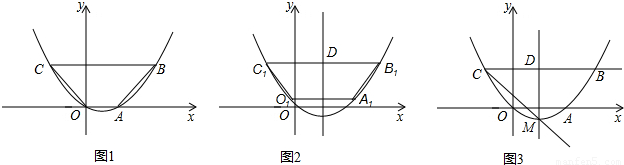
 ;
; .
. 不合题意,舍去,所以分两种情况讨论:①当0<t<
不合题意,舍去,所以分两种情况讨论:①当0<t<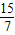 时,由题意知△FQE∽△FAG,得∠FGA=∠FEQ,由于BC∥x轴,则∠DPQ=∠FGA=∠FEQ,由此可证得△DPQ∽△DEB,DB、DE的长已求得,可用t表示出DP、DQ的长,根据相似三角形所得比例线段,即可求得此时t的值;
时,由题意知△FQE∽△FAG,得∠FGA=∠FEQ,由于BC∥x轴,则∠DPQ=∠FGA=∠FEQ,由此可证得△DPQ∽△DEB,DB、DE的长已求得,可用t表示出DP、DQ的长,根据相似三角形所得比例线段,即可求得此时t的值; <t<3
<t<3 时,方法同①;
时,方法同①; ,
, ,
, x2-
x2- x;
x;
 x22-
x22- x2-
x2- x12+
x12+ x1=3,
x1=3, (x2+x1)-
(x2+x1)- ]=3①,
]=3①, =3(x1+x2)-6,
=3(x1+x2)-6, +2②,
+2②,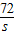 (S>0),
(S>0),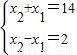 ,
,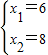 ,
, ×62-
×62- ×6=3,
×6=3, 秒,可使直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似.理由如下:
秒,可使直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似.理由如下: x-
x- ,可得直线AB与对称轴的交点E的坐标为(1,-
,可得直线AB与对称轴的交点E的坐标为(1,- ),
), ,DP=5-t,DQ=t,
,DP=5-t,DQ=t, =
= ,
, =
= ,解得t=
,解得t= .
. 时,如图3-1;
时,如图3-1; ,即
,即 =
= ,
, >
> ,
, 不合题意,舍去;
不合题意,舍去; ②当
②当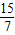 <t<3
<t<3 时,如图3-2;
时,如图3-2; ,即
,即 =
= ,
, ,符合题意.
,符合题意. 秒时,直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似.
秒时,直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似.

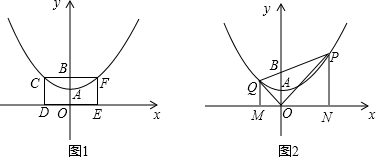

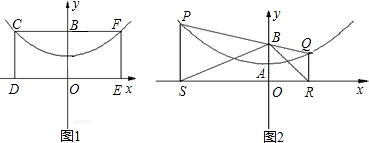 轴上,CF交y轴于点B(0,2),且其面积为8.
轴上,CF交y轴于点B(0,2),且其面积为8.