
【题目】如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E. 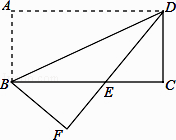
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长.
【答案】
(1)证明:∵AD∥BC,
∴∠ADB=∠DBC,
根据折叠的性质∠ADB=∠BDF,∠F=∠A=∠C=90°,
∴∠DBC=∠BDF,
∴BE=DE,
在△DCE和△BFE中,
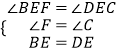 ,
,
∴△DCE≌△BFE
(2)解:在Rt△BCD中,
∵CD=2,∠ADB=∠DBC=30°,
∴BC=2 ![]() ,
,
在Rt△ECD中,
∵CD=2,∠EDC=30°,
∴DE=2EC,
∴(2EC)2﹣EC2=CD2,
∴CE= ![]() ,
,
∴BE=BC﹣EC= ![]()
【解析】(1)由AD∥BC,知∠ADB=∠DBC,根据折叠的性质∠ADB=∠BDF,所以∠DBC=∠BDF,得BE=DE,即可用AAS证△DCE≌△BFE;(2)在Rt△BCD中,CD=2,∠ADB=∠DBC=30°,知BC=2 ![]() ,在Rt△BCD中,CD=2,∠EDC=30°,知CE=
,在Rt△BCD中,CD=2,∠EDC=30°,知CE= ![]() ,所以BE=BC﹣EC=
,所以BE=BC﹣EC= ![]() .
.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:初中数学 来源: 题型:
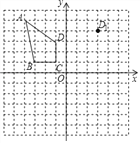
【题目】如图所示,在网格中建立平面直角坐标系,每个小正方形的边长都是1个单位长度,四边形ABCD的各顶点均在网格点上.
(1)将四边形ABCD平移,使得D点平移到D1(3,4),画出平移后的四边形A1B1C1D1;
(2)画出四边形ABCD绕着原点O逆时针旋转90°后的四边形A2B2C2D2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式的规律,解答下列问题:
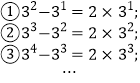
(1)按此规律,第④个等式为_________;第![]() 个等式为_______;(用含
个等式为_______;(用含![]() 的代数式表示,
的代数式表示,![]() 为正整数)
为正整数)
(2)按此规律,计算:
![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
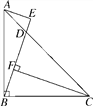
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC,D是AC上一点,AE⊥BD,交BD的延长线于E,CF⊥BD于F.
(1)求证:CF=BE;
(2)若BD=2AE,求证:∠EAD=∠ABE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,若AB=4,E是AD边上一点(点E与点A、D不重合),BE的中垂线交AB于点M,交DC于点N,设AE=x,BM=y,则y与x的大致图象是( )

A. B.
B. C.
C. D.
D.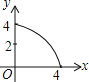
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图①中△ABC是等边三角形,其边长是3,图②中△DEF是等腰直角三角形,∠F=90°,DF=EF=3.
(1)若S1为△ABC的面积,S2为△DEF的面积,S3=![]() AB·BC·sinB,S4=
AB·BC·sinB,S4=![]() DE·DF·sinD,请通过计算说明S1与S3,S2与S4之间有着怎样的关系;
DE·DF·sinD,请通过计算说明S1与S3,S2与S4之间有着怎样的关系;
![]()
(2)在图③中,∠P=α(α为锐角),OP=m,PQ=n,△OPQ的面积为S,请你根据第(1)小题的解答,直接写出S与m,n以及α之间的关系式,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长与面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”国庆期间出租车司机小李某天下午的营运始终在长安街(自东向西或自西向东)上进行,如果规定向东为正,向西为负,他这天下午从天安门出发,行车里程(单位:千米)如下:
+15,﹣2,+5,﹣1,+10,﹣3,﹣2,+12,+4,﹣5,+6.
(1)小李将最后一名乘客送抵目的地时,小李距天安门有多远?
(2)如果汽车耗油量为0.08升/千米,这天下午小李共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l上依次有三点A、B、C,且AB=8、BC=16,点P为射线AB上一动点,将线段AP进行翻折得到线段PA’(点A落在直线l上点A’处、线段AP上的所有点与线段PA’上的点对应)如图1
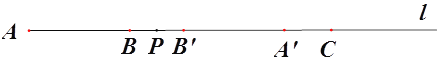
(1)若翻折后A’C=2,则翻折前线段AP= ;
(2)若点P在线段BC上运动,点M为线段A’C的中点,求线段PM的长度;
(3)若点P 在线段BC上运动,点N为B’P的中点,点M为线段A’C的中点,设AP=x,用x表示A’M+PN.

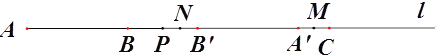
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com