C
分析:根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD,然后根据等边对等角的性质求出∠ABD,再根据三角形的内角和定理以及等腰三角形两底角相等求出ABC、∠C的度数,再求出∠CBD,然后对各选项分析判断后利用排除法求解.
解答:∵MN是AB的中垂线,
∴AD=BD,
∴∠ABD=∠A=36°,
∵AB=AC,∠A=36°,
∴∠ABC=∠C=

(180°-36°)=72°,
∴∠CBD=∠ABC-∠ABD=72°-36°=36°,
∴∠ABD=∠CBD,射线BD是△ABC是角平分线,故①正确;
在△BCD中,∠BDC=180°-∠CBD-∠C=180°-36°-72°=72°,
∴∠C=∠BDC,
∴△BCD是等腰三角形,
等腰三角形还有△ABC,△ABD,共3个,故②正确;
△BCD的周长=BC+CD+BD=BC+CD+AD=AB+BC,故③正确;
④△AMD是有一个锐角是36°的直角三角形,△BCD是顶角为36°的等腰三角形,两三角形不全等,故本小题错误;
综上所述,正确的有①②③共3个.
故选C.
点评:本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质,等腰三角形的判定与性质,全等三角形的判定,根据度数相等求得相等的角是解题的关键.

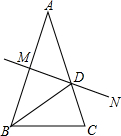 如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于M,有下面4个结论:
如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于M,有下面4个结论: (180°-36°)=72°,
(180°-36°)=72°,
