
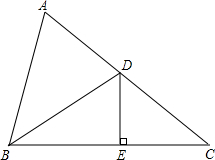
 如图:△ABC中,BA=BD,DE垂直平分BC,∠ABD=40°,则∠C=35°.
如图:△ABC中,BA=BD,DE垂直平分BC,∠ABD=40°,则∠C=35°. 分析 根据三角形内角和定理和等腰三角形性质求出∠BDA,根据线段垂直平分线得出BD=DC,求出∠C=∠CBD,根据三角形外角性质求出∠BDA=2∠C,代入求出即可.
解答 解:∵AB=AD,∠ABD=40°,
∴∠BDA=∠A=$\frac{1}{2}$(180°-∠ABD)=70°,
∵DE垂直平分BC,
∴BD=DC,
∴∠C=∠DBC,
∴∠BDA=∠C+∠CBD=2∠C=70°,
∴∠C=35°
故答案为:35°.
点评 本题考查了三角形内角和定理,等腰三角形性质,线段垂直平分线性质的应用,能求出∠BDA的度数和BD=CD是解此题的关键,注意:线段垂直平分线上的点到线段两个端点的距离相等.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:填空题
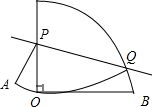 如图,是一个圆心角为90°的扇形,AO=2cm,点P在半径AO上运动,点Q在弧AB上运动,沿PQ将它以上的部分向下翻折,使翻折后的弧恰好过点O,则OP的最大距离为$\frac{2\sqrt{3}}{3}$.
如图,是一个圆心角为90°的扇形,AO=2cm,点P在半径AO上运动,点Q在弧AB上运动,沿PQ将它以上的部分向下翻折,使翻折后的弧恰好过点O,则OP的最大距离为$\frac{2\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,若双曲线y=$\frac{k}{x}$与边长为5的等边△AOB的边OA、AB分别相交于C、D两点,且OC=3BD.则实数k的值为$\frac{9\sqrt{3}}{4}$.
如图,若双曲线y=$\frac{k}{x}$与边长为5的等边△AOB的边OA、AB分别相交于C、D两点,且OC=3BD.则实数k的值为$\frac{9\sqrt{3}}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com