
| A. | 335 | B. | 336 | C. | 670 | D. | 671 |
分析 根据题意分别利用当x=$\frac{1}{3}$时,当x=$\frac{1}{2}$时,当x=$\frac{2}{3}$时…求出M的值,进而得出数字变化规律,进而得出不超过2014的“隐形数”的个数.
解答 解:∵M=[x]+[2x]+[3x],将不能表示成M形式的正整数称为“隐形数”,
∴当x=$\frac{1}{3}$时,M=0+0+1=1,
当x=$\frac{1}{2}$时,M=0+1+1=2,
当x=$\frac{2}{3}$时,M=0+1+2=3,
当x=1时,M=1+2+3=6,
当x=1$\frac{1}{3}$时,M=1+2+4=7,
当x=$\frac{3}{2}$时,M=1+3+4=8,
当x=$\frac{5}{3}$时,M=1+3+5=9,
当x=2时,M=2+4+6=12,
当x=2$\frac{1}{3}$时,M=2+4+7=13,
当x=$\frac{5}{2}$时,M=2+5+7=14,
当x=$\frac{8}{3}$时,M=2+5+8=15,
当x=3时,M=3+6+9=18,
…
即每6个数有2个“隐形数”,
∵2014÷6=335…4,前4个数只有一个“隐形数”,
∴不超过2014的“隐形数”的个数是:335×2+1=671.
故选:D.
点评 此题主要考查了取整计算,根据题意分别得出M的值的变化规律是解题关键.


科目:初中数学 来源: 题型:解答题
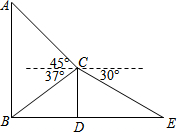 某班数学兴趣小组为了测量建筑物AB的高度,他们选取了地面上一点E,测得DE的长度为8.65米,并以建筑物CD的顶端点C为观测点,测得点A的仰角为45°,点B的俯角为37°,点E的俯角为30°.
某班数学兴趣小组为了测量建筑物AB的高度,他们选取了地面上一点E,测得DE的长度为8.65米,并以建筑物CD的顶端点C为观测点,测得点A的仰角为45°,点B的俯角为37°,点E的俯角为30°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
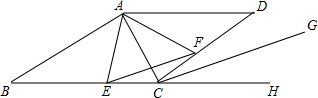
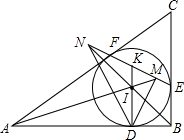 如图,△ABC的内切圆I在边AB,BC,CA上的切点分别是D,E,F,直线EF与直线AI,BI,DI分别相交于点M,N,K.
如图,△ABC的内切圆I在边AB,BC,CA上的切点分别是D,E,F,直线EF与直线AI,BI,DI分别相交于点M,N,K.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
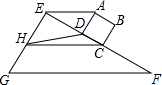 如图,正方形ABCD的边CD与Rt△EFG的直角边EF重合,将正方形ABCD以1cm/s的速度沿FE方向移动,在移动过程中,边CD始终与边EF重合(移动开始时点C与点F重合).连接AE,过点C作AE的平行线交直线EG于点H,连接HD.已知正方形 ABCD 的边长为1cm,EF=4cm,设正方形移动时间为x(s),线段EH的长为y(cm),其中0≤x≤2.5.
如图,正方形ABCD的边CD与Rt△EFG的直角边EF重合,将正方形ABCD以1cm/s的速度沿FE方向移动,在移动过程中,边CD始终与边EF重合(移动开始时点C与点F重合).连接AE,过点C作AE的平行线交直线EG于点H,连接HD.已知正方形 ABCD 的边长为1cm,EF=4cm,设正方形移动时间为x(s),线段EH的长为y(cm),其中0≤x≤2.5. 查看答案和解析>>
科目:初中数学 来源: 题型:选择题
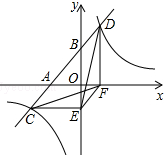 如图,一次函数y=ax+b与x轴、y轴交于A、B两点,与反比例函数y=$\frac{k}{x}$相交于C、D两点,分别过C、D两点作y轴、x轴的垂线,垂足为E、F,连接CF、DE、EF. 有下列三个结论:①△CEF与△DEF的面积相等;②△DCE≌△CDF;③AC=BD.其中正确的结论个数是( )
如图,一次函数y=ax+b与x轴、y轴交于A、B两点,与反比例函数y=$\frac{k}{x}$相交于C、D两点,分别过C、D两点作y轴、x轴的垂线,垂足为E、F,连接CF、DE、EF. 有下列三个结论:①△CEF与△DEF的面积相等;②△DCE≌△CDF;③AC=BD.其中正确的结论个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com