
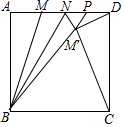
 如图,正方形ABCD的边长为6,AM=$\frac{1}{3}$AD,点N在线段MD上,连接BN,把△BMN沿BN翻折,得到△BM′N,延长BM′交线段DN于点P,连接CM′,DM′,当△CDM′是等腰三角形时,MN的长为$\frac{131-24\sqrt{65}}{8}$或=$\frac{19\sqrt{31}+16}{54}$.
如图,正方形ABCD的边长为6,AM=$\frac{1}{3}$AD,点N在线段MD上,连接BN,把△BMN沿BN翻折,得到△BM′N,延长BM′交线段DN于点P,连接CM′,DM′,当△CDM′是等腰三角形时,MN的长为$\frac{131-24\sqrt{65}}{8}$或=$\frac{19\sqrt{31}+16}{54}$. 分析 分两种情形讨论:①如图1中,当CM′=CD=6时,作M′E⊥AD于E,EM′交BC于F,z则四边形EFCD是矩形,设DE=CF=x.由FM′2=BM′2-BF2=CM′2-CF2,可得40-(6-x)2=36-x2,求出x的值,在Rt△ENM′中,设MN=NM′=y,利用勾股定理列出方程即可.②如图2中,当CM′=DM′时,作M′E⊥AD于E,EM′交BC于F,作M′H⊥CD于H,则四边形EFCD是矩形,CH=HD=3,设MN=NM′=x.在Rt△NEM′中,利用勾股定理列出方程即可解决问题.
解答 解:①如图1中,当CM′=CD=6时,作M′E⊥AD于E,EM′交BC于F,z则四边形EFCD是矩形,设DE=CF=x.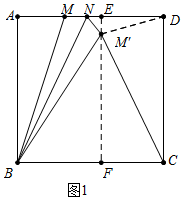
在Rt△ABM中,∵∠A=90°.AB=6,AM=2,
∴BM=BM′=$\sqrt{{2}^{2}+{6}^{2}}$=$\sqrt{40}$,
∵FM′2=BM′2-BF2=CM′2-CF2,
∴40-(6-x)2=36-x2,
∴x=$\frac{8}{3}$,
∴FM′=$\sqrt{CM{′}^{2}-C{F}^{2}}$=$\frac{2\sqrt{65}}{3}$,
∴EM′=6-$\frac{2\sqrt{65}}{3}$,设MN=NM′=y,
在Rt△ENM′中,y2=(6-$\frac{2\sqrt{65}}{3}$)2+(4-y-$\frac{8}{3}$)2,
解得y=$\frac{131-24\sqrt{65}}{8}$.
②如图2中,当CM′=DM′时,作M′E⊥AD于E,EM′交BC于F,作M′H⊥CD于H,则四边形EFCD是矩形,CH=HD=3,设MN=NM′=x.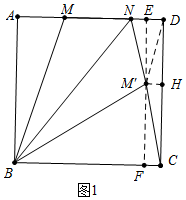
在Rt△BFM′中,BF=$\sqrt{CM{′}^{2}-FM{′}^{2}}$=$\sqrt{40-9}$=$\sqrt{31}$,
∴CF=DE=6-$\sqrt{31}$,
在Rt△NEM′中,x2=32+(4-x-6+$\sqrt{31}$)2,
解得x=$\frac{19\sqrt{31}+16}{54}$.
综上所述,当△CDM′是等腰三角形时,MN的长为$\frac{131-24\sqrt{65}}{8}$或$\frac{19\sqrt{31}+16}{54}$.
点评 本题考查正方形的性质、翻折变换、勾股定理、等腰三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,学会用方程的思想思考问题,属于中考填空题中的压轴题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
| x | 3.23 | 3.24 | 3.25 | 3.26 |
| ax2+bx+c | -0.06 | -0.02 | 0.03 | 0.09 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
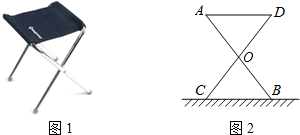
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 先向左平移2个单位长度,再向下平移2个单位长度 | |
| B. | 先向左平移2个单位长度,再向上平移2个单位长度 | |
| C. | 先向右平移2个单位长度,再向下平移2个单位长度 | |
| D. | 先向右平移2个单位长度,再向上平移2个单位长度 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
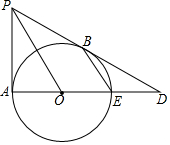 如图,PA,PB分别与⊙O相切于点A,B,延长PB交直径AE的延长线于点D.
如图,PA,PB分别与⊙O相切于点A,B,延长PB交直径AE的延长线于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com