
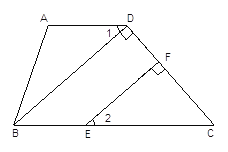
【题目】如图,在四边形ABCD中,∠A=104°-∠2,∠ABC=76°+∠2,BD⊥CD于D,EF⊥CD于F.
求证:∠1=∠2.请你完成下面证明过程.
证明:因为∠A=104°-∠2,∠ABC=76°+∠2,( )
所以 ∠A+∠ABC=104°-∠2+76°+∠2, ( 等式性质 )
即 ∠A+∠ABC=180°
所以 AD∥BC,( )
所以 ∠1=∠DBC,( )
因为 BD⊥DC,EF⊥DC,( )
所以 ∠BDC=90°,∠EFC=90°,( )
所以 ∠BDC=∠EFC,
所以 BD∥ ,( )
所以 ∠2=∠DBC,( )
所以 ∠1=∠2 ( ).
【答案】见解析.
【解析】首先观察已知条件中的角,不难发现:两个角互补,得平行.再根据平行线的性质得到有关角之间的关系,运用等量代换的方法证明最后的结论.
证明:因为∠A=104°-∠2,∠ABC=76°+∠2,(已知 )
所以∠A+∠ABC=104°-∠2+76°+∠2, ( 等式性质 )
即 ∠A+∠ABC=180°
所以 AD∥BC,(同旁内角互补,两直线平行)
所以 ∠1=∠DBC,(两直线平行,内错角相等)
因为 BD⊥DC,EF⊥DC,(已知)
所以 ∠BDC=90°,∠EFC=90°,( 垂直定义)
所以 ∠BDC=∠EFC,
所以 BD∥EF,(同位角相等,两直线平行)
所以 ∠2=∠DBC,(两直线平行,同位角相等)
所以 ∠1=∠2 (等量代换).



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知,关于 x,y 的方程组![]() 的解满足 x<0,y>0.
的解满足 x<0,y>0.
(1)x= ,y= (用含 a 的代数式表示);
(2)求 a 的取值范围;
(3)若 2x8y=2m,用含有 a 的代数式表示 m,并求 m 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班师生组织植树活动,上午8时从学校出发,到植树地点后原路返校,如图为师生离校路程s与时间t之间的图象,请回答下列问题:
![]() 试写出师生返校时的s与t的函数关系式,并求出师生何时回到学校;
试写出师生返校时的s与t的函数关系式,并求出师生何时回到学校;
![]() 如果师生骑自行车上午8时出发,到植树地点后,植树需2小时,要求14时前返回到学校,往返平均速度分别为每时10km、8km,现有A、B、C、D四个植树点与学校的路程分别是13km、15km、17km、19km,试通过计算说明哪几个植树点符合要求.
如果师生骑自行车上午8时出发,到植树地点后,植树需2小时,要求14时前返回到学校,往返平均速度分别为每时10km、8km,现有A、B、C、D四个植树点与学校的路程分别是13km、15km、17km、19km,试通过计算说明哪几个植树点符合要求.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,完全平方式可以用平面几何图形的面积来表示。实际上还有一些代数恒等式也可以用这种形式表示,如:(2a+b)(a+b)=2a2+3ab+b2,就可以用图(1)或图(2)等图形的面积表示。

(1)请写出图(3)所表示的代数恒等式: ;
(2)试画一个几何图形,使它的面积表示:(a+b)(a+2b)=a2+3ab+2b2;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司承接A、B两种货物运输业务,已知3月份A货物运费单价为50元/吨,B货物运费单价为30元/吨,共收取运费9500元;4月份由于工人工资上涨,运费单价上涨情况为:A货物运费单价增加了40%,B货物运费单价上涨到40元/吨;该物流公司4月承接的A种货物和B种货物的数量与3月份相同,4月份共收取运费13000元.试求该物流公司3月份运输A、B两种货物各多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作与探究 探索:在如图1至图3中,△ABC的面积为a .
(1)如图1, 延长△ABC的边BC到点D,使CD=BC,连结DA.若△ACD的面积为S1,则S1=________(用含a的代数式表示);




(2)如图2,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连结DE.若△DEC的面积为S2,则S2= (用含a的代数式表示);
(3)在图2的基础上延长AB到点F,使BF=AB,连结FD,FE,得到△DEF(如图3).若阴影部分的面积为S3,则S3=__________(用含a的代数式表示).
发现:像上面那样,将△ABC各边均顺次延长一倍,连结所得端点,得到△DEF(如图3),此时,我们称△ABC向外扩展了一次.可以发现,扩展一次后得到的△DEF的面积是原来△ABC面积的_____倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司试销一种成本为30元/件的新产品,按规定试销时的销售单价不低于成本单价,又不高于80元/件,试销中每天的销售量y(件)与销售单价x(元/件)满足下表中的函数关系.
(1)试求y与x之间的函数表达式;(2)设公司试销该产品每天获得的毛利润为S(元),求S与x之间的函数表达式(毛利润=销售总价-成本总价);
(2)当销售单价定为多少时,该公司试销这种产品每天获得的毛利润最大?
(3)最大毛利润是多少?此时每天的销售量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地,设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示
(1)求甲车从A地到达B地的行驶时间;
(2)求甲车返回时y与x之间的函数关系式,并写出自变量x的取值范围;
(3)求乙车到达A地时甲车距A地的路程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com