
【题目】如图,已知△ABC中,AB=AC=12cm,∠B=∠C,BC=8cm,点D为AB的中点.
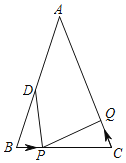
(1)如果点P在线段BC上以2cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,则经过 后,点P与点Q第一次在△ABC的 边上相遇?(在横线上直接写出答案,不必书写解题过程)
【答案】(1)①①△BPD≌△CPQ,理由见解析;②3cm/s;(2)24秒,AC
【解析】
(1)①△BPD≌△CPQ,利用已知条件求出BP=CQ,PC=BD.利用SAS证明△BPD≌△CQP.
②由点Q的运动速度与点P的运动速度不相等,所以BP≠CQ,又由△BPD与△CPQ全等,∠B=∠C,得到BP=PC=4cm,CQ=BD=6cm,从而求出点P,点Q运动的时间为4÷2=2秒,即可解答.
(2)设经过t秒后,点P与点Q第一次相遇.由题意:3t﹣2t=24,求出x即可解决问题;
解:(1)①△BPD≌△CPQ,
理由如下∵t=1s,
∴BP=CQ=2×1=2cm,
∵AB=12cm,点D为AB的中点,
∴BD=6cm.
又∵PC=BC﹣BP,BC=8cm,
∴PC=8﹣2=6cm,
∴PC=BD.
又∵AB=AC,
∴∠B=∠C,
在△BPD和△CPQ中,
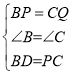 ,
,
∴△BPD≌△CQP(SAS).
②∵点Q的运动速度与点P的运动速度不相等,
∴BP≠CQ,
又∵△BPD与△CPQ全等,∠B=∠C,
∴BP=PC=4cm,CQ=BD=6cm,
∴点P,点Q运动的时间为4÷2=2s,
∴Q点的运动速度为6÷2=3(cm/s).
(2)设经过t秒后,点P与点Q第一次相遇.
由题意:3t﹣2t=24,
∴t=24,
∴24×3=72,
∵△ABC的周长为32,
∴点P与点Q第一次相遇在AC边上.
故答案为24秒,AC.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】一块含45°的直角三角板ABC, AB=AC, ∠BAC=90°, 点D为射线CB上一点,且不与点C,点B重合,连接AD.过点A作线段AD的垂线l,在直线l上,截取AE=AD(点E与点C在直线AD的同侧),连接CE.
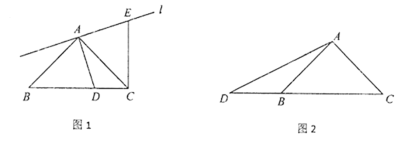
(1)当点D在线段CB上时,如图1,线段CE与BD的数量关系为____________,位置关系为___________;
(2)当点D在线段CB的延长线上时,如图2,
①请将图形补充完整;
②(1)中的结论是否仍成立?如果成立,请证明;如果不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=14,DE是线段AB的垂直平分线.
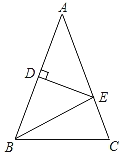
(1)若△EBC的周长是24,求BC的长;
(2)若∠A=x°,求∠EBC的度数(用含x的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,AC的垂直平分线DE交AC于点D,交BC于点E,且∠BAE=90°,若DE=1,则BE=( )
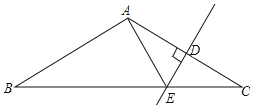
A.4B.3C.2D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦放假期间,小明和小华准备到西安的大雁塔(记为A)、白鹿原(记为B)、兴庆公园(记为C)、秦岭国家植物园(记为D)中的一个景点去游玩,他们各自在这四个景点中任选一个,每个景点被选中的可能性相同
(1)求小明选择去白鹿原游玩的概率;
(2)用树状图或列表的方法求小明和小华选择去同一个地方游玩的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com