
【题目】如图,在△ABC中,AB=BC,∠ABC=90°,点F为AB延长线上一点,点E在BC上,BE=BF,连接AE,EF和CF.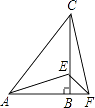
(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠EFC的度数.
【答案】
(1)证明:∵∠ABC=90°,F为AB延长线上一点,
∴∠ABC=∠CBF=90°.
在△ABE和△CBF中,
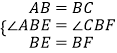 ,
,
∴△ABE≌△CBF
(2)解:∵在△ABC中,AB=BC,∠ABC=90°,点F为AB延长线上一点,点E在BC上,BE=BF,
∴△ABC和△EBF都是等腰直角三角形,
∴∠ACB=∠EFB=45°.
∵∠CAE=30°,
∴∠AEB=∠CAE+∠ACB=30°+45°=75°.
由(1)知△ABE≌△CBF,
∴∠CFB=∠AEB=75°.
∴∠EFC=∠CFB﹣∠EFB=75°﹣45°=30°
【解析】(1)根据已知条件由SAS得到△ABE≌△CBF;(2)由已知可得△ABC和△EBF都是等腰直角三角形,再根据由(1)知△ABE≌△CBF,求出∠EFC的度数.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC且BD>CD,DF⊥AB,△CDE和△ADB都是等腰直角三角形,给出下列结论,正确的是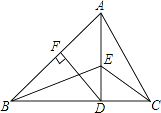
①△ADC≌△BDE;
②△ADF≌△BDF;
③△CDE≌△AFD;
④△ACE≌ABE.
查看答案和解析>>
科目:初中数学 来源: 题型:
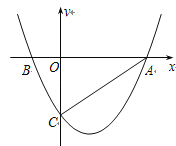
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于C点,已知A(3,0),且M(1,
与x轴交于A、B两点,与y轴交于C点,已知A(3,0),且M(1,![]() )是抛物线上另一点.
)是抛物线上另一点.
(1)求a、b的值;
(2)连结AC,设点P是y轴上任一点,若以P、A、C三点为顶点的三角形是等腰三角形,求P点的坐标;
(3)若点N是x轴正半轴上且在抛物线内的一动点(不与O、A重合),过点N作NH∥AC交抛物线的对称轴于H点.设ON=t,△ONH的面积为S,求S与t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某沿海开放城市A接到台风警报,在该市正南方向100km的B处有一台风中心,沿BC方向以20km/h的速度向D移动,已知城市A到BC的距离AD=60km,那么台风中心经过多长时间从B点移到D点?如果在距台风中心30km的圆形区域内都将有受到台风的破坏的危险,正在D点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险?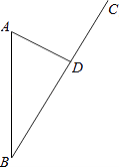
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com