
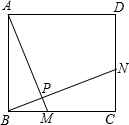
 如图,点M,N分别是正方形ABCD的边BC,CD上的点,且BM=CN,AM与BN交于点P,试探索AM与BN的关系.
如图,点M,N分别是正方形ABCD的边BC,CD上的点,且BM=CN,AM与BN交于点P,试探索AM与BN的关系.分析 (1)由正方形的性质得出∠ABM=∠BCN=90°,AB=BC,由SAS证明△ABM≌△BCN,得出对应边相等即可;
(2)由全等三角形的性质得出∠BAM=∠NBC,由角的互余关系得出∠APB=90°,即可得出AM⊥BN.
解答 (1)解:AM=BN;理由如下:
∵四边形ABCD是正方形
∴∠ABM=∠BCN=90°,AB=BC,
在△ABM和△BCN中,$\left\{\begin{array}{l}{AB=BC}&{\;}\\{∠ABM=∠BCN}&{\;}\\{BM=CN}&{\;}\end{array}\right.$,
∴△ABM≌△BCN(SAS),
∴AM=BN;故答案为:
(2)解:AM⊥BN;理由如下:
由(1)得:△ABM≌△BCN,
∴∠BAM=∠NBC,
∵∠NBC+∠ABN=∠ABC=90°,
∴∠BAM+∠ABN=90°,
在△ABP中,∠APB=180°-(∠BAM+∠ABN)=90°,
∴AM⊥BN;
故答案为:AM⊥BN.
点评 本题考查了正方形的性质、全等三角形的判定与性质;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=1,b=3,c=2,d=4 | B. | a=4,b=6,c=5,d=10 | ||
| C. | a=2,b=4,c=3,d=6 | D. | a=2,b=3,c=4,d=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形DAB的面积为9.
如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形DAB的面积为9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
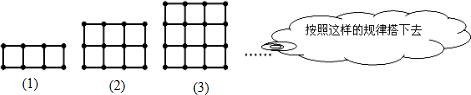
| 图形编号 | (1) | (2) | (3) | (4) | (5) | (6) |
| 火柴棒根数 | 10 | 17 | 24 | 31 | 38 | 45 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
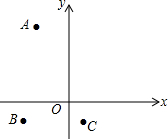 在平面直角坐标系中,点A、B、C的坐标分别是A(-2,5),B(-3,-1),C(1,-1)找一点D,使四边形ABCD是平行四边形,求点D的坐标.
在平面直角坐标系中,点A、B、C的坐标分别是A(-2,5),B(-3,-1),C(1,-1)找一点D,使四边形ABCD是平行四边形,求点D的坐标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com