练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．已知关于x的方程$\frac{x+m}{x-3}$=m无解，求m的值．

    分析 分式方程去分母转化为整式方程，根据分式方程无解得到x-3=0，求出x=3，代入整式方程即可求出m的值．

    解答 解：分式方程去分母得：x+m=m（x-3），
    x（1-m）=-4m
    由分式方程无解得到x-3=0，即x=3，
    代入整式方程得：m=-3．
    当1-m=0时，即m=1时，整式方程x（1-m）=-4m无解，
    ∴m=1或-3．

    点评 此题考查了分式方程的解，解决本题的关键是熟记分式方程的解即为能使分式方程左右两边相等的未知数的值，且分式方程分母不为0．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    14．如图，OP平分∠AOB，∠AOP=15°，PC∥OA，PD⊥OA于点D，PC=4，则PD=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．如表是我市4个区县今年5月31日最高气温（℃）的统计结果：
    永定区武陵源区慈利县桑植县
    32323330
    该日最高气温的众数和中位数分别是（　　）
    A．32℃，32℃B．32℃，33℃C．33℃，33℃D．32℃，30℃

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，点C在线段AB上，AC=8cm，CB=6cm，点M，N分别是AC，BC的中点．求线段MN的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

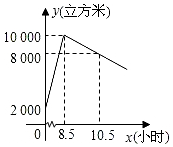    14．星期天8：00～8：30，燃气公司给加气站的储气罐注入天然气．之后，一位工作人员以每车20立方米的加气量，依次给在加气站排队等候的若干辆车加气．储气罐中的储气量y（立方米）与时间x（小时）的函数关系如图所示．
    （1）8：00～8：30，燃气公司向储气罐注入了多少立方米的天然气；
    （2）当x≥0.5时，求储气罐中的储气量y（立方米）与时间x（小时）的函数解析式；
    （3）请问给第16辆车加完气用了多长时间？说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．将方程4x+3y=6变形成用y的代数式表示x，则x=$\frac{6-3y}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．在平面直角坐标系中，已知抛物线C1：y=a（x-3）2过点（0，1），顶点为P，将抛物线C1向下平移h（h＞0）个单位长度得到抛物线C2
    过点M（0，m2）（m＞0）作直线l平行于x轴，与两抛物线从左到右分别相交于A，B，C，D四点，若A，C两点关于y轴对称，点G在抛物线C1上，四边形APCG是平行四边形．
    （1）求a的值；
    （2）求证：点M为PG中点；
    （3）求m的值；
    （4）求抛物线C2的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．化简求值：（7x2-6xy+1）-2（3x2-4xy）-5，其中x=-1，y=-$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

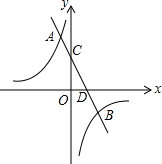    9．如图，在平面直角坐标系xOy中，一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于点A（-1，6）和点B（3，m），与y轴交于点C，与x轴交于点D．
    （1）求一次函数y=k1x+b和反比例函数y=$\frac{{k}_{2}}{x}$的表达式；
    （2）点P是双曲线y=$\frac{{k}_{2}}{x}$上的一点，且满足S△PCD=S△DOC，求点P的坐标．

    查看答案和解析>>

    同步练习册答案