
先阅读下面解方程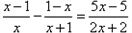 的过程,然后回答后面的问题。
的过程,然后回答后面的问题。
解:第一步:将原方程整理为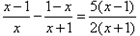
第二步:方程两边同除以(x-1),得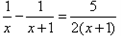
第三步:去分母,得2(x+1)+2x=5x
第四步:解这个整式方程得x=2。
上面解题过程中:
(1)第三步变形的依据是 。
(2)出现错误的一步是 。
(3)上述解题过程中还缺少的一步是 。
(4)方程的正确解为 。
科目:初中数学 来源: 题型:阅读理解
| x |
| x-1 |
| x |
| x-1 |
查看答案和解析>>
科目:初中数学 来源:2010-2011学年山东省潍坊市诸城市繁华中学九年级(上)月考数学试卷(10月份)(解析版) 题型:解答题
 .
.查看答案和解析>>
科目:初中数学 来源:《28.3 用一元二次方程解决实际问题》2010年习题精选(二)(解析版) 题型:解答题
 .
.查看答案和解析>>
科目:初中数学 来源:2009-2010学年河南省南阳市书院中学九年级(上)第一学月数学试卷(解析版) 题型:解答题
 .
.查看答案和解析>>
科目:初中数学 来源:2006年青海省中考数学试卷(课标卷)(解析版) 题型:解答题
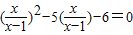 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com