
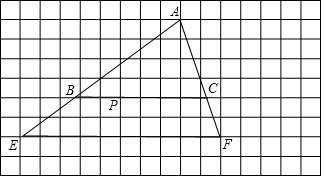
���� ��1����AH��EF��H����BC��G����BC��EF���Ƴ���ABC�ס�AEF���ɵ�$\frac{BC}{AF}$=$\frac{AG}{AH}$���г����̼��ɽ�����⣮
��2��ȡEF���е�T������AT��BC��P����ʱPAƽ�֡�ABC�������
��� �⣺��1����AH��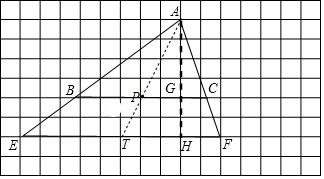 EF��H����BC��G��
EF��H����BC��G��
��BC��EF��
���ABC�ס�AEF��
��$\frac{BC}{AF}$=$\frac{AG}{AH}$��
��$\frac{BC}{10}$=$\frac{4}{6}$��
��BC=$\frac{20}{3}$��
�ʴ�Ϊ$\frac{20}{3}$��
��2��ȡEF���е�T������AT��BC��P����ʱPAƽ�֡�ABC�������
���ɣ���BC��EF��
��$\frac{BP}{ET}$=$\frac{AP}{AT}$=$\frac{PC}{TF}$��
��ET=TF��
��BP=PC��
��S��ABP=S��APC��
��ֱ��PA��Ϊ����
���� ���⿼����ͼ��Ӧ�á����ɶ��������������ε��ж������ʡ������ε����ߵ����ʵ�֪ʶ������Ĺؼ���ѧ�����ӳ��ø����ߣ��������������ε����ʽ�����⣬�����п��������ͣ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 31Ԫ | B�� | 30.2Ԫ | C�� | 29.7Ԫ | D�� | 27Ԫ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
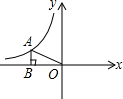 ��ͼ����AΪ����������y=$\frac{k}{x}$ͼ����һ�㣬��A��AB��x���ڵ�B������OA���ABO�����Ϊ4��k=-8��
��ͼ����AΪ����������y=$\frac{k}{x}$ͼ����һ�㣬��A��AB��x���ڵ�B������OA���ABO�����Ϊ4��k=-8���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
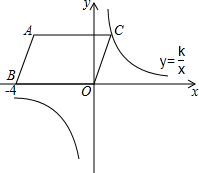 ��ͼ����ƽ��ֱ������ϵ�У��ı���ABOCΪƽ���ı��Σ�A��B������ֱ�Ϊ��-3��3������-4��0��������һ˫����y=$\frac{k}{x}$��ͼ����C��������˫���ߵı���ʽΪy=$\frac{3}{x}$��
��ͼ����ƽ��ֱ������ϵ�У��ı���ABOCΪƽ���ı��Σ�A��B������ֱ�Ϊ��-3��3������-4��0��������һ˫����y=$\frac{k}{x}$��ͼ����C��������˫���ߵı���ʽΪy=$\frac{3}{x}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У���֪������y=ax2+bx-2��a��0����x�ύ��A��1��0����B��3��0�����㣬��y�ύ�ڵ�C���䶥��Ϊ��D����E������Ϊ��0��-1��������������BE������һ��F������BC��
��ͼ����ƽ��ֱ������ϵ�У���֪������y=ax2+bx-2��a��0����x�ύ��A��1��0����B��3��0�����㣬��y�ύ�ڵ�C���䶥��Ϊ��D����E������Ϊ��0��-1��������������BE������һ��F������BC���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com