Question

【题目】在平面直角坐标系中，抛物线y=x2+（k﹣1）x﹣k与直线y=kx+1交于A、B两点，点A在点B的左侧．

（1）如图1，当k=1时，直接写出A，B两点的坐标；

（2）在（1）的条件下，点P为抛物线上的一个动点，且在直线AB下方，试求出△ABP面积的最大值及此时点P的坐标；

（3）如图2，抛物线y=x2+（k﹣1）x﹣k（k＞0）与x轴交于点C、D两点（点C在点D的左侧），是否存在实数k使得直线y=kx+1与以O、C为直径的圆相切？若存在，请求出k的值；若不存在，请说明理由．

Answer 1

【答案】（1）A（﹣1，0），B（2，3）（2）点P坐标为（，﹣）（3）k=时，使得直线y=kx+1与以O、C为直径的圆相切

【解析】试题分析：（1）当k=1时，联立抛物线与直线的解析式，解方程求得点A、B的坐标；
（2）如图2，作辅助线，求出△ABP面积的表达式，然后利用二次函数的性质求出最大值及点P的坐标；
（3）设以OC为直径的圆与直线AB相切于点Q，由圆周角定理可知，此时以此为基础，构造相似三角形，利用比例式列出方程，求得k的值．

试题解析：(1)当k=1时,抛物线解析式为 直线解析式为y=x+1.

联立两个解析式 得：

解得：x=1或x=2，

当x=1时，y=x+1=0；当x=2时，y=x+1=3，

∴A(1,0),B(2,3).

(2)设

如答图2所示,过点P作PF∥y轴,交直线AB于点F,则F(x,x+1).

∴

∴

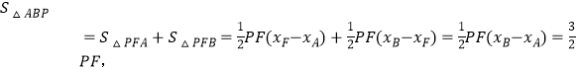
当时,

∴△ABP面积最大值为,此时点P坐标为

(3)设直线AB:y=kx+1与x轴、y轴分别交于点E.F，

则

在Rt△EOF中,由勾股定理得：

令 即(x+k)(x1)=0，解得：x=k或x=1.

∴C(k,0)，OC=k.

设以OC为直径的圆与直线AB相切于点Q,根据圆周角定理,此时 如图3所示，

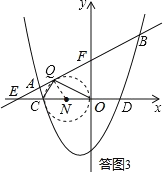
设点N为OC中点,连接NQ,则NQ⊥EF,

∴

∵

∴△EQN∽△EOF，

∴ 即：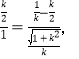

解得：

∵k>0，

∴

即存在实数k使得直线与以O、C为直径的圆相切.