
【题目】在平面直角坐标系中,A(0,1),B(5,0)将线段AB向上平移到DC,如图1,CD交y轴于点E,D点坐标为(﹣2,a)
(1)直接写出点C坐标(C的纵坐标用a表示);
(2)若四边形ABCD的面积为18,求a的值;
(3)如图2,F为AE延长线上一点,H为OB延长线上一点,EP平分∠CEF,BP平分∠ABH,求∠EPB的度数.

【答案】(1)C(3,a﹣1).(2)a=5.(3)∠EPB=45°.
【解析】
(1)利用平移的性质解决问题即可.
(2)根据S平行四边形ABCD=S△CDH+S△CBH﹣S△ADH﹣S△AHB,构建方程即可解决问题.
(3)如图2中 作AM∥EP交BP于M.求出∠AMB即可解决问题.
解:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵点A向上平移a﹣1个单位,向左平移2个单位得到点D,
∴点B(5,0)向上平移a﹣1个单位,向左平移2个单位得到点C,
∴C(3,a﹣1).
(2)如图1中,如图1中,作DH⊥x轴于H.连接CH,AH.
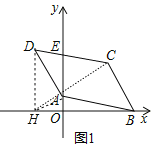
∵S平行四边形ABCD=S△CDH+S△CBH﹣S△ADH﹣S△AHB,
∴![]() a5+
a5+![]() ×7(a﹣1)﹣
×7(a﹣1)﹣![]() a2﹣
a2﹣![]() ×7×1=18,
×7×1=18,
解得a=5.
(3)如图2中 作AM∥EP交BP于M.
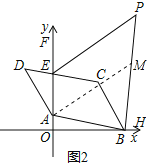
∵EC∥AB,
∴∠FEC=∠FAB,
∵PE∥AM,
∴∠FEP=∠FAM,
∵EP平分∠FEC,
∴∠FEP=![]() ∠FEC,
∠FEC,
∴∠FAM=![]() ∠FAB,
∠FAB,
∵BP平分∠ABH,
∴∠ABP=![]() ∠ABH,
∠ABH,
∴∠MAB+∠ABM=![]() (∠FAB+∠ABH)=
(∠FAB+∠ABH)=![]() (∠AOB+∠ABO+∠OAB+∠AOB)=
(∠AOB+∠ABO+∠OAB+∠AOB)=![]() (180°+90°)=135°,
(180°+90°)=135°,
∴∠AMB=180°﹣(∠MAB+∠ABM)=45°,
∵AM∥PE,
∴∠EPB=∠AMB=45°.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD是菱形,点A的坐标为(0,![]() ),分别以A,B为圆心,大于
),分别以A,B为圆心,大于![]() AB的长为半径作弧,两弧交于点E,F,直线EF恰好经过点D,则点D的坐标为( )
AB的长为半径作弧,两弧交于点E,F,直线EF恰好经过点D,则点D的坐标为( )
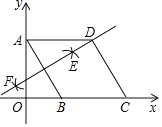
A. (2,2)B. (2,![]() )C. (
)C. (![]() ,2)D. (
,2)D. (![]() +1,
+1,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=-![]() x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限作等边△ABC.
x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限作等边△ABC.
(1)若点C在反比例函数y=![]() 的图象上,求该反比例函数的解析式;
的图象上,求该反比例函数的解析式;
(2)点P(2![]() ,m)在第一象限,过点P作x轴的垂线,垂足为D,当△PAD与△OAB相似时,P点是否在(1)中反比例函数图象上?如果在,求出P点坐标;如果不在,请加以说明.
,m)在第一象限,过点P作x轴的垂线,垂足为D,当△PAD与△OAB相似时,P点是否在(1)中反比例函数图象上?如果在,求出P点坐标;如果不在,请加以说明.
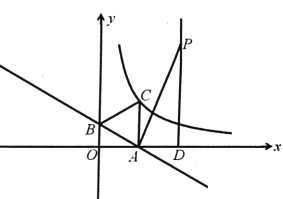
查看答案和解析>>
科目:初中数学 来源: 题型:
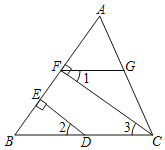
【题目】填空,将理由补充完整.
如图,CF⊥AB于F,DE⊥AB于E,∠1+∠EDC=180°,求证:FG∥BC
证明:∵CF⊥AB,DE⊥AB(已知)
∴∠BED=∠BFC=90°(垂直的定义)
∴ED∥FC ( )
∴∠2=∠3 ( )
∵∠1+∠EDC=180°(已知)
又∵∠2+∠EDC=180°(平角的定义)
∴∠1=∠2 ( )
∴∠1=∠3(等量代换)
∴FG∥BC ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】威丽商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元?
(2)由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按x元/公里计算,耗时费按y元/分钟计算(总费用不足9元按9元计价).小明、小刚两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与打车时间如表:
时间(分钟) | 里程数(公里) | 车费(元) | |
小明 | 8 | 8 | 12 |
小刚 | 12 | 10 | 16 |
(1)求x,y的值;
(2)如果小华也用该打车方式,打车行驶了11公里,用了14分钟,那么小华的打车总费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
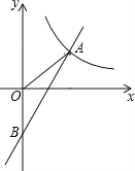
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求一次函数y=kx+b和y=![]() 的表达式;
的表达式;
(2)已知点C在x轴上,且△ABC的面积是8,求此时点C的坐标;
(3)反比例函数y=![]() (1≤x≤4)的图象记为曲线C1,将C1向右平移3个单位长度,得曲线C2,则C1平移至C2处所扫过的面积是_________.(直接写出答案)
(1≤x≤4)的图象记为曲线C1,将C1向右平移3个单位长度,得曲线C2,则C1平移至C2处所扫过的面积是_________.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB,点C在直线AB上,D为线段BC的中点.
(1)若AB=8 ,AC=2,求线段CD的长.
![]()
(2)若点E是线段AC的中点,直接写出线段DE和AB的数量关系是________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com