【题目】如图，△ABC和△CDE都是等边三角形，则下列结论不成立的是（ ）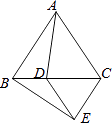 
A.∠BDE=120°
B.∠ACE=120°
C.AB=BE
D.AD=BE
【答案】B
【解析】解：∵△CDE都是等边三角形， ∴∠CDE=60°，
∴∠BDE=180°﹣∠CDE=120°，故A正确；
∵△ABC和△CDE都是等边三角形，
∴∠ACB=60°，∠DCE=60°，
∴∠ACE=∠ACB+∠DCE=60°+60°=120°，故B正确；
∵△ABC和△CDE都是等边三角形，
∴AC=BC，EC=DC，∠ACD=∠BCE=60°．
在△ACD和△BCE中，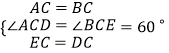
，
∴△ACD≌△BCE（SAS），
∴AD=BE．故D正确；
∵△ABD与△EBD不全等，
∴AB≠BE．
故选：B．
【考点精析】利用等边三角形的性质对题目进行判断即可得到答案，需要熟知等边三角形的三个角都相等并且每个角都是60°．
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AB=AC=10cm，BC=8cm，点D为AB的中点，点P在线段BC上以3cm/s的速度由点B向点C移动，同时，点Q在线段CA上由点C向点A移动．若点Q的移动速度与点P的移动速度相同，则经过秒后，△BPD≌△CQP．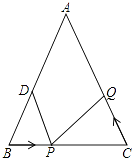 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，∠AOB的内部有一点P，在射线OA，OB边上各取一点P1 ， P2 ， 使得△PP1P2的周长最小，作出点P1 ， P2 ， 叙述作图过程（作法），保留作图痕迹．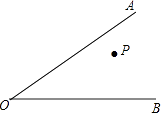 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知△ABC的∠ABC和∠ACB的平分线BE，CF交于点G，若∠BGC=115°，则∠A= ．
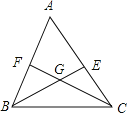
【答案】50°
【解析】
试题分析：根据三角形内角和定理求出∠GBC+∠GCB，根据角平分线的定义求出∠ABC+∠ACB，根据三角形内角和定理计算即可．
解：∵∠BGC=115°，
∴∠GBC+∠GCB=180°﹣115°=65°，
∵BE，CF是△ABC的∠ABC和∠ACB的平分线，
∴∠GBC=
ABC，∠GCB=ACB，
∴∠ABC+∠ACB=130°，
∴∠A=180°﹣130°=50°，
故答案为：50°．
【题型】填空题
【结束】
14
【题目】如图所示，有（1）～（4）4个条形方格图，图中由实线围成的图形与前图全等的有
________（只要填序号即可）．
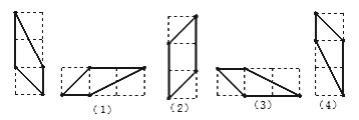
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把两个含有45°角的直角三角板如图放置，点D在AC上，连接AE、BD，试判断AE与BD的关系，并说明理由．
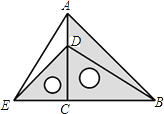
【答案】BF⊥AE，理由详见解析.
【解析】BD=AE ,BD⊥AE.延长BD交AE于F ,证△BCD≌△ACE,可得BD=AE ,BD⊥AE .
∵CE=CD，CA=CB，∠ACE=∠BCD=90°，∴△BCD≌△ACE，∴BD=AE，∠CBD=∠CAE，∵∠CAE+∠AEC=90°，∴∠CBD+∠AEC=90°，∴∠BFE=90°，即BD⊥AE.
【题型】解答题
【结束】
24
【题目】在△ABC中，已知∠B=50°，∠C=60°，AE⊥BC于E，AD平分∠BAC；求：∠DAE的度数．
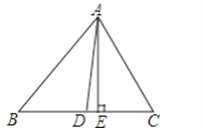
查看答案和解析>>
科目：初中数学 来源： 题型：
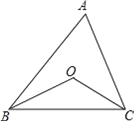
【题目】如图，已知点O是△ABC的两条角平分线的交点，
（1）若∠A=30°，则∠BOC的大小是 ；
（2）若∠A=60°，则∠BOC的大小是 ；
（3）若∠A=n°，则∠BOC的大小是多少？试用学过的知识说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读材料：若x2－2xy＋2y2－8y＋16＝0，求x、y的值．
解：∵x2－2xy＋2y2－8y＋16＝0，
∴（x2－2xy＋y2）＋（y2－8y＋16）＝0
∴（x－y）2＋（y－4）2＝0，
∴（x－y）2＝0，（y－4）2＝0，
∴y＝4，x＝4．
根据你的观察，探究下面的问题：
已知a、b满足a2＋b2－4a－6b＋13＝0．求a、b的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】A、B两地相距450千米，甲、乙两车分别从A、B两地同时出发，相向而行．已知甲车的速度为120千米/时，乙车的速度为80千米/时，t时后两车相距50千米，则t的值为____________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
