
如图,以Rt△ABC的一条直角边AB为直径作⊙O,与AC交于点F,在AB的延长线上取一点E,联结EF与BC交于点D,且使得DF=CD.
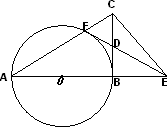
(1)求证:FE是⊙O的切线
(2)如果sin∠A=![]() ,AE=
,AE=![]() ,求AF的长
,求AF的长
|
(1)证明:联结OF ∵OA=OF ∴∠OAF=∠OFA ∵DF=DC.∴∠DFC=∠DCF…………………………1分 ∵∠ABC=90° ∴∠OAF+∠FCD=90° ∴∠AFO+∠DFC=90° ∴∠OFD=90°……………………2分 ∴CD与⊙O相切…………………………3分
(2)∵sin∠A= 在Rt△ABC和Rt△CBE中,∠A=30°,∠BEF=30° 设BD=x,则BE= ∴AC=4x∴AB=2 ∴x= ∴AC= 联结BF,则有DF= 又∵∠BFC=90°∴DB=DF=DC, ∵∠ACB=60° ∴△DFC为等边三角形 ∴CF=DF= ∴AF=AC-CF=1……………………5分 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 23、如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连接ED、BD.
23、如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连接ED、BD.查看答案和解析>>
科目:初中数学 来源: 题型:
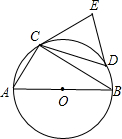 已知,如图,以Rt△ABC的斜边AB为直径作⊙0,D是BC上的点,且有弧AC=弧CD,连CD、BD,在BD延长线上取一点E,使∠DCE=∠CBD.
已知,如图,以Rt△ABC的斜边AB为直径作⊙0,D是BC上的点,且有弧AC=弧CD,连CD、BD,在BD延长线上取一点E,使∠DCE=∠CBD.| 5 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2009•黔南州)如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连接DE.
(2009•黔南州)如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连接DE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com